Задание 4

Пример 1

Задача

Для кодирования некоторой последовательности, состоящей из букв Л, М, Н, П, Р, решили использовать неравномерный двоичный код, удовлетворяющий условию, что никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Для букв Л, М, Н использовали соответственно кодовые слова 00, 01, 11. Для двух оставшихся букв – П и Р – кодовые слова неизвестны. Укажите кратчайшее возможное кодовое слово для буквы П, при котором код будет удовлетворять указанному условию. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Построим дерево для заданного двоичного кода:

для того чтобы выполнить условие Фано (ни одно кодовое слово не совпадает с началом другого кодового слова), необходимо, чтобы все буквы размещались в листьях дерева

у нас осталась единственная свободная ветка 10, на которую нужно «навесить» две буквы; это можно сделать так:

таким образом, для кода буквы П есть два варианта одной длины: 100 и 101; по условию выбираем вариант с меньшим значением, то есть 100

Ответ: 100

Пример 2

Задача

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 10, 11. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Построим дерево для заданного двоичного кода:

согласно условию Фано, код декодируется однозначно, если все используемые кодовые слова соответствуют листьям такого дерева; видим, что для заданных кодовых слов это условие выполняется

может показаться, что ответ – 01, поскольку на эту ветвь можно «подвесить» букву Д, однако это не так – тогда будет некуда подвешивать оставшуюся букву – Е

поэтому для того, чтобы добавить в это дерево две буквы (Д и Е) и сохранить выполнение условия Фано, нужно в узле 01 сделать развилку, тогда получается два свободных кода, 010 и 011, из них меньший – 010

Ответ: 010

Пример 3

Задача

По каналу связи с помощью равномерного двоичного кода передаются сообщения, содержащие только 4 буквы: X, Y, Z, W; для кодировки букв используются кодовые слова длины 5. При этом для набора кодовых слов выполнено такое свойство: любые два слова из набора отличаются не менее чем в трёх позициях. Это свойство важно для расшифровки сообщений при наличии помех. Для кодирования букв X, Y, Z используются 5-битовые кодовые слова: X: 01111, Y: 00001, Z: 11000. Определите 5-битовое кодовое слово для буквы W, если известно, что оно начинается с 1 и заканчивается 0.

По условию кодовое слово для буквы W соответствует маске 1***0, где вместо звёздочек можно поставить 0 или 1.

Найдем расстояния Хэмминга – количество позиций, в которых отличается это кодовое слово от известных кодовых слов букв X, Y и Z:

X: 01111  Y: 00001   Z: 11000
W: 1***0  W: 1***0   W: 1***0
    2+?       2+?        0+?

Знаки вопроса обозначают неизвестные неотрицательные числа – количество различающихся позиций в тех битах, которые в кодовом слове для буквы W неизвестны.

Как видим, наиболее критичная ситуация сложилась для пары Z-W. Для того, чтобы эти кодовые слова различались в трёх позициях, все неизвестные биты кодового слова буквы W должны иметь значения, обратные соответствующим битам кодового слова для буквы Z, то есть, W = 10110

Проверяем полученное кодовое слово: находим расстояние Хэмминга в парах X-W и Y-W:

X: 01111  Y: 00001   Z: 11000
W: 10110  W: 10110   W: 10110
     3         4          3

Как видим, для все пар расстояние не меньше трёх, что соответствует условию задачи.

Ответ: 10110

Пример 4

Задача

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0; дл буквы Б – кодовое слово 10. Какова наименьшая возможная сумма длин всех шести кодовых слов? Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.

это задание удобнее решать с помощью дерева; условие Фано выполняется тогда, когда все выбранные кодовые слова заканчиваются в листьях дерева

построим дерево по известным кодовым словам: А – 0, Б – 10:

на оставшуюся свободную ветку нужно «повесить» 4 кодовых слова (для букв В, Г, Д, Е)

если выбрать один код длиной 3 (В – 110), то оставшиеся 3 кода нужно «повесить» на одну ветку, так, что на ней нужно делать две развилки:

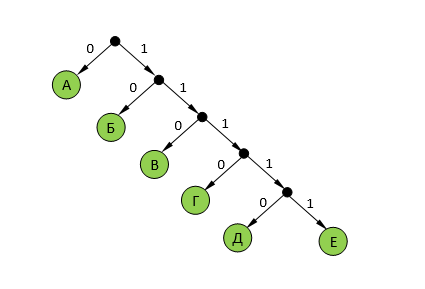
суммарная длина кодовых слов будет в этом случае равна

$$1 + 2 + 3 + 4 + 2 * 5 = 20$$

попробуем другой вариант: оставшиеся 4 кода повесить на 4 ветки одинаковой длины:

суммарная длина кодовых слов будет в этом случае меньше, чем в предыдущем случае:

$$1 + 2 + 4*4 = 19$$

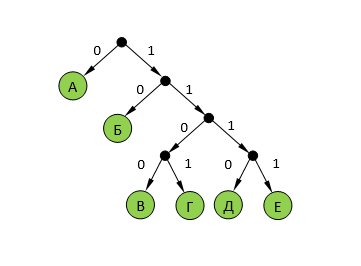
Ответ: 19

Пример 5

Задача

По каналу связи передаются сообщения, каждое из которых содержит 16 букв А, 8 букв Б, 4 буквы В и 4 буквы Г (других букв в сообщениях нет). Каждую букву кодируют двоичной последовательностью. При выборе кода учитывались два требования:

а) ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование);

б) общая длина закодированного сообщения должна быть как можно меньше.

Какой код из приведённых ниже следует выбрать для кодирования букв А, Б, В и Г?

1) А:0, Б:10, В:110, Г:111

2) А:0, Б:10, В:01, Г:11

3) А:1, Б:01, В:011, Г:001

4) А:00, Б:01, В:10, Г:11

сначала выберем коды, в которых ни одно кодовое слово не совпадет с началом другого (такие коды называю префиксными)

для кода 2 условие «а» не выполняется, так как кодовое слово буквы В (01) начинается с кодового слова буквы А (0)

для кода 3 условие «а» не выполняется, так как кодовое слово буквы В (011) начинается с кодового слова буквы Б (01)

для кодов 1 и 4 условие выполняется, их рассматриваем дальше

считаем общее количество битов в сообщении для кода 1:

$$16*1 + 8*2 + 4*3 + 4*3 = 56 битов$$

считаем общее количество битов в сообщении для кода 4:

$$16*2 + 8*2 + 4*2 + 4*2 = 64 бита$$

код 1 даёт наименьшую длину сообщения, поэтому выбираем его

Ответ: 1

Пример 6

Задача

По каналу связи передаются сообщения, содержащие только 5 букв А, И, К, О, Т. Для кодирования букв используется неравномерный двоичный код с такими кодовыми словами: А - 0, И - 00, К - 10, О - 110, Т - 111. Среди приведённых ниже слов укажите такое, код которого можно декодировать только одним способом. Если таких слов несколько, укажите первое по алфавиту.

прежде всего заметим, что для заданного кода не выполняется ни прямое, ни обратное условие Фано; «виновата» в этом пара А – И: код буквы А совпадает как с началом, так и с окончанием кода буквы И; больше ни для одной пары кодовых слов прямое условие Фано не нарушено

это означает, что не все сообщения могут быть декодированы однозначно

теперь нужно понять, какие последовательности могут быть декодированы неоднозначно; в данном случае очевидно, что сообщения АА и И кодируются одинаково: 00, поэтому все слова, где есть АА или И, не могут быть декодированы однозначно

поэтому варианты 1 (КАА) и 2 (ИКОТА) отпадают

на всякий случай проверим вариант 3: КОТ = 10110111; первой буквой может быть только К (по-другому сочетание 10 получить нельзя), аналогично вторая буква – только О, а третья – только Т

Ответ: 3

Пример 7

Задача

По каналу связи передаются сообщения, содержащие только 4 буквы: Е, Н, О, Т. Для кодирования букв Е, Н, О используются 5-битовые кодовые слова: Е - 00000, Н - 00111, О - 11011. Для этого набора кодовых слов выполнено такое свойство: любые два слова из набора отличаются не менее чем в трёх позициях. Это свойство важно для расшифровки сообщений при наличии помех. Какое из перечисленных ниже кодовых слов можно использовать для буквы Т, чтобы указанное свойство выполнялось для всех четырёх кодовых слов?

1) 11111

2) 11100

3) 00011

4) не подходит ни одно из указанных выше слов

код, рассмотренный в условии задачи, относится к помехоустойчивым кодам, которые позволяют обнаружить и исправить

определенное количество ошибок, вызванных помехами при передаче данных;

количество позиций, в которых отличаются два кодовых слова одинаковой длины, называется расстоянием Хэмминга

код, в котором расстояние Хэмминга между каждой парой кодовых слов равно d, позволяет обнаружить до d-1 ошибок;

для исправления r ошибок требуется выполнение условия

$$d \geq 2r + 1$$

поэтому код с $d = 3$ позволяет обнаружить одну или две ошибки, и исправить одну ошибку.

легко проверить, что для заданного кода (Е - 00000, Н - 00111, О - 11011) расстояние Хэмминга равно 3; в таблице

выделены отличающиеся биты, их по три в парах Е-Н и Н-О и четыре в паре Е-О:

      Е – 00000     Е – 00000       Н – 00111
      Н – 00111     О – 11011       О – 11011

теперь проверяем расстояние между известными кодами и вариантами ответа; для первого ответа 11111 получаем минимальное расстояние 1 (в паре О-Т), этот вариант не подходит:

       Е – 00000        Н – 00111       О – 11011
       Т - 11111        Т - 11111       Т - 11111

для второго ответа 11100 получаем минимальное расстояние 3 (в парах Е-Т и О-Т):

       Е – 00000        Н – 00111       О – 11011
       Т - 11100        Т - 11100       Т - 11100

для третьего ответа 00011 получаем минимальное расстояние 1 (в паре Н-Т) , этот вариант не подходит:

       Е – 00000        Н – 00111       О – 11011
       Т - 00011        Т - 00011       Т - 00011

таким образом, расстояние Хэмминга, равное 3, сохраняется только для ответа 2

Ответ: 2

Пример 8

Задача

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А–00, Б–010, В–011, Г–101, Д–111. Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.

1) для буквы Б – 01

2) это невозможно

3) для буквы В – 01

4) для буквы Г – 01

для однозначного декодирования достаточно, чтобы выполнялось условие Фано или обратное условие Фано;

проверяем последовательно варианты 1, 3 и 4; если ни один из них не подойдет, придется выбрать вариант 2 («это невозможно»);

проверяем вариант 1: А–00, Б–01, В–011, Г–101, Д–111. «прямое» условие Фано не выполняется (код буквы Б совпадает с началом кода буквы В); «обратное» условие Фано не выполняется (код буквы Б совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит;

проверяем вариант 3: А–00, Б–010, В–01, Г–101, Д–111. «прямое» условие Фано не выполняется (код буквы В совпадает с началом кода буквы Б); «обратное» условие Фано не выполняется (код буквы В совпадает с окончанием кода буквы Г); поэтому этот вариант не подходит;

проверяем вариант 4: А–00, Б–010, В–011, Г–01, Д–111. «прямое» условие Фано не выполняется (код буквы Г совпадает с началом кодов букв Б и В); но «обратное» условие Фано выполняется (код буквы Г не совпадает с окончанием кодов остальных буквы); поэтому этот вариант подходит;

Ответ: 4

Пример 9

Задача

Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Если таким способом закодировать последовательность символов БАВГ и записать результат шестнадцатеричным кодом, то получится

1) $4B_{16}$

2) $411_{16}$

3) $BACD_{16}$

4) $1023_{16}$

Шестнадцатеричным код - это число, записанное в шестнадцатиричной системе счисления. Про системы счисления написано здесь

из условия коды букв такие: A – 00, Б –01, В – 10 и Г – 11, код равномерный

последовательность БАВГ кодируется так: 01 00 10 11 = 1001011

разобьем такую запись на тетрады справа налево и каждую тетраду переведем в шестнадцатеричную систему (то есть, сначала в десятичную, а потом заменим все числа от 10 до 15 на буквы A, B, C, D, E, F); получаем $1001011_2 = 4B_{16}$

Ответ: 1

Пример 10

Задача

Черно-белое растровое изображение кодируется построчно, начиная с левого верхнего угла и заканчивая в правом нижнем углу. При кодировании 1 обозначает черный цвет, а 0 – белый.

Для компактности результат записали в шестнадцатеричной системе счисления. Выберите правильную запись кода.

1) BD9AA5

2) BDA9B5

3) BDA9D5

4) DB9DAB

«вытянем» растровое изображение в цепочку: сначала первая (верхняя) строка, потом – вторая, и т.д.:

в этой полоске 24 ячейки, черные заполним единицами, а белые – нулями:

поскольку каждая цифра в шестнадцатеричной системе раскладывается ровно в 4 двоичных цифры, разобьем полоску на тетрады – группы из четырех ячеек (в данном случае все равно, откуда начинать разбивку, поскольку в полоске целое число тетрад – 6):

переводя тетрады в шестнадцатеричную систему, получаем последовательно цифры B (11), D(13), A(10), 9, D(13) и 5, то есть, цепочку BDA9D5

Ответ: 3

Задания для самостоятельного выполнения