Теория

Натуральные числа - это в первую очередь количество тех или иных предметов. Чтобы изобразить это количество на бумаге, требуется использовать ту или иную систему счисления. Говоря о натуральных числах в смысле количества предполагается множество $\mathbb{N}_0$, т.е. объединение математического множества натуральных чисел с нулём (эквивалентом отсутствия предметов)

У каждой системы счисления есть своё основание - набор кникальных знаков, каждый из которых соответствует тому или иному количеству. Например, в общепринятой десятиричной системе счисления основание - это числа от $0$ до $9$.

Если количество больше символа, соответствующего максимальному значению, тогда слева добавляются разряды - такие же символы, но подразумевающие, что количество сопоставляется с соответствующим знаком, но при этом оно должно быть домножено на количество, большее максимально определяемого знаками на 1. Эта величина называется основанием.

Основание указывается с помощью нижнего индекса у записываемой величины. Например, число $13_{10}$ записывается в двоичной системе $1101_2$, а в шестнадцатиричной - $D_{16}$.

Обратите внимание

Система счисления - это всего лишь способ записи количества

Если основание системы равно 10, т.е. записано обычное число, то его можно разложить по разрядам:

Точно также можно разложить число в двоичной системе

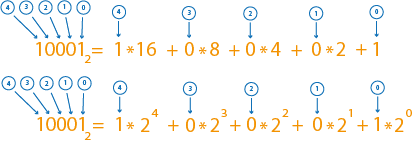
В принципе, любое число можно разложить по любому основанию, но это выходит за рамки задач егэ.

Разряд, стоящий с левого края называет старшим, с правого - младшим.

У числа $153_{10}$ старший разряд - второй, его значение равно $1$, младший - нулевой, его значение равно $3$. У числа $10001_2$ значение старшего равно $1$, младшего - тоже.

Перевод между системами счисления

Чтобы перевести число из одной системы в другую, используются готовые алгоритмы.

Конечно, есть алгоритм перевода любой системы в любую, но алгоритмы перевода в десятеричную систему и из неё гораздо проще. Поэтому если требуется перевести из одной недесятеричной системы в другую недесятеричную, лучше перевести число из первой системы в десятеричную, а потом из десятеричной во вторую.

Системы счисления до 10 строятся одинаковым образом: основание просто определяет диапазон цифр, которые можно использовать в записи числа. Однако в программировании очень популярна шестнадцатеричная система счисления. Из названия следует, что в каждом разряде может быть 16 значений.

Чтобы записать 16 значений, к 10 цифрам просто добавили 6 первых букв латинского алфавита.

В таблице приведено соответствие между буквами и значениями

A	B	C	D	E	F
10	11	12	13	14	15

Перевод в десятеричную систему

По сути, мы уже рассмотрели перевод в десятеричную систему, когда рассматривали разложение по разрядам чисел $153_{10}$ и $10001_2$.

Общая идея заключается в том, что мы нумеруем разряды с нуля от младшего к старшему, после чего каждое значение разряда домножаем на основание, возведённое в степень, равную порядковому номеру разряда.

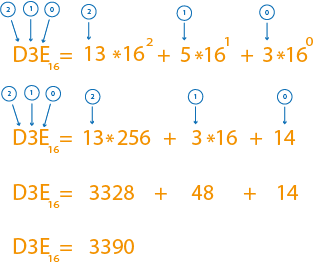
В нашем случае основание $16$, поэтому у старшего разряда под номером 2 множитель равен $16^2=256$, у первого разрада множитель равен просто $16$, а у нулевого - $0$

Перевод из десятеричной системы

Перевод из десятеричной системы в другую немного сложнее. Здесь необходимо не умножать, а делить.

Раз за разом необходимо делить число в столбик, пока частное не станет меньше делителя.

Переведём таким способом $1835_{10}$ в семеричную систему

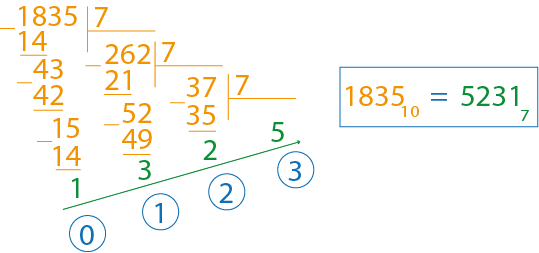
Остатки необходимо запоминать и потом объединить воедино. Очень важен порядок. Первый полученный остаток необходимо поставить на место нулевого разряда, второй остаток - на место первого разряда и т.д.

В итоге получим ответ:

$1835_{10}=5231_7$

Общий случай

Рассмотрим теперь, как перевести число из одной недесятеричной системы в другую.

В качестве примера переведём число $31334_5$ в шестнадцатеричную.

Для этого сначала переведём его в десятеричную систему счисления, а потом полученное число уже в шестнадцатеричную.

$31334_5=2094_{10}$

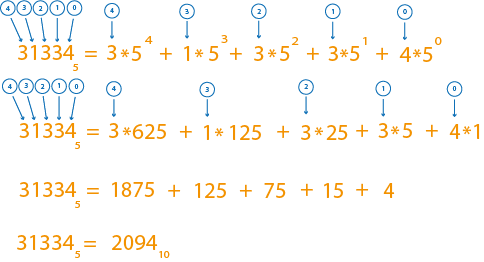
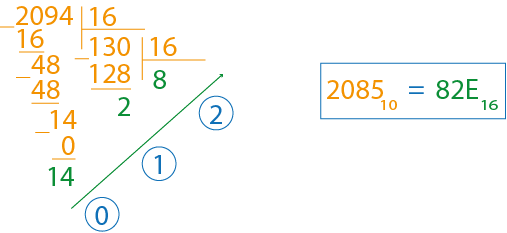
Получим: $2094_{10}=82E_{16}$.

danger

Обратите внимание: вместо числа 14 в младший разряд я поставил букву $E$.

Ответ: $82E_{16}$

Лайфхаки

Если число заканчивается на $n$ нулей, тогда оно делится нацело на число, равное основанию, взятому в степени $n$.

Например, если в двоичном числе значения двух младших разрядов - нули, то оно делится нацело на 4.

Например, $1001101000_2$ делится нацело на $2^3$, т.к. первое ненулевое слагаемое содержит в качестве множителя основание $2$ в степени $3$.

По тем же соображениям число $F100_{16}$ делится нацело на $16$.

Быстрый перевод

Если основание одной системы является точной степенью другого, то между переход между ними выполняется гораздо проще.

Чтобы перейти от одной системы, достаточно перевести каждый символ в системе с большим основанием по отдельности в систему с меньшим основанием, а потом соединить результаты в том же порядке, как шли исходные символы.

Переведём по такому алгоритму число $3F01_{16}$ в двоичную систему счисления. Т.к. $16=2^4$, то на каждый символ исходного числа нам необходимо выделить по 4 в новом числе

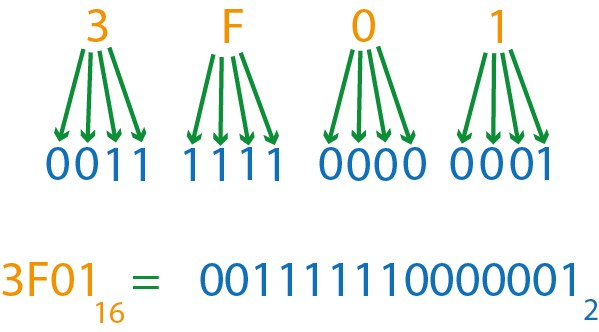
В итоге получим $3F01_{16}=001111110000001_2$

Если необходимо выполнить преобразование в обратную сторону, то число в исходной системе счисления разбивается, начиная с младшего разряда, на блоки по столько знаков, в какой степени основание исходной системы счисления равно основанию новой.

Переведём теперь число $1011101_2$ в восьмеричную систему счисления.

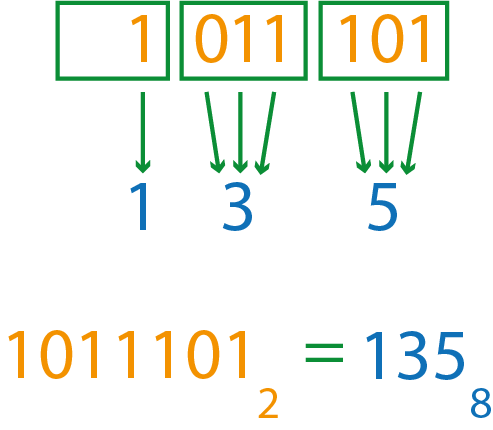
В итоге получим $1011101_2=135_8$

Калькулятор

В операционной системе Windows есть встроенный калькулятор. В нём есть инструменты для работы в разных системах счисления. Самым полезным для сдачи егэ является автоматический перевод из одной системы счисления в другую.

Нажмите кнопку Win на клавиатуре и введите calc

В списке появится приложение Калькулятор, запустите его.

Если у вас стоит англоязычная система, то калькулятор может выглядеть так

Работа с системами счисления доступная в режиме "Программист".

Чтобы в него перейти, кликните по трём палочкам

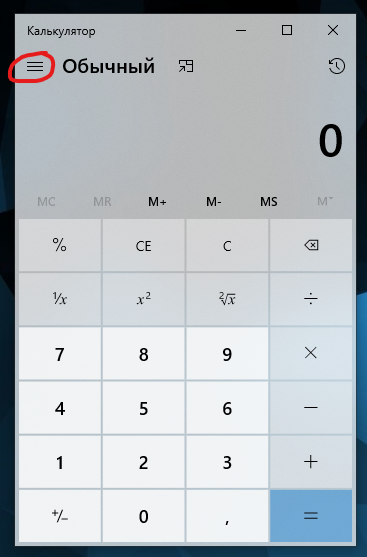
В появившемся меню выберите пункт "Программист"

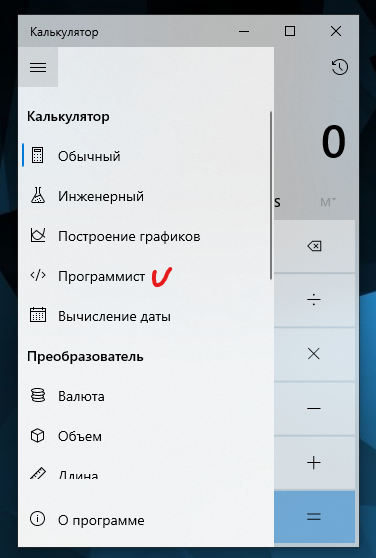
В этом режиме можно впрямую указывать, в какой системе счисления работать.

Я выделил блок перехода между системами. Просто кликните по любому из пунктов - система перейдёт в режим работы с соответствующим основанием.

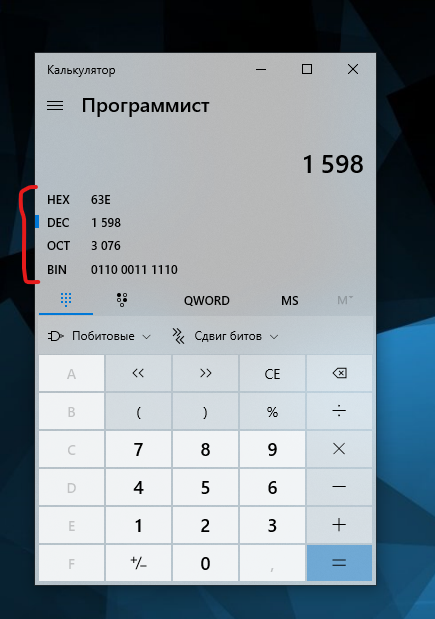
Я перешёл в систему с основанием 8. На клавиатуре калькулятора доступны только цифры от $0$ до $7$.

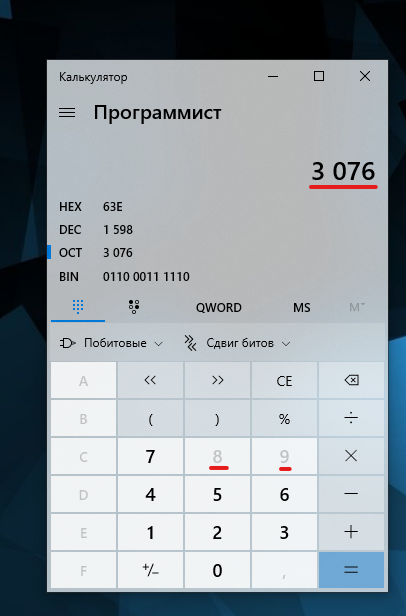
HEX - шестнадцатеричная система счисления, DEC - десятеричная, OCT - восьмеричная, BIN = двоичная.

Бит чётности

В некоторых задачах задействован бит чётности. Это - самый простой способ проверки, правильно ли доставлены данные. Ведь во время передачи по сети могут наводиться помехи, техника может сбоить, поэтому тот или иной бит может передаться неправильно.

Чтобы контролировать передачу, вводят некоторую операцию над всеми битами, а её результат добавляют в конец последовательности бит. Такая операция чаще всего называется вычисление контрольной суммы. Бит чётности - это тоже контрольная сумма.

Он вычисляется следующим образом: считается количество единиц в последовательности, после чего вычисляется её остаток от деления на 2. Результат записывается справа, т.е. все разряды увеличиваются на 1, а в младший записывается результат.

Дополнение числа битом чётности будем обозначать $B(x)$, тогда

$$B(1001101_2)=10011010_2,~ B(100101_2)=1001011_2$$

Цифры из числа

Возможно, вам хватит калькулятора Windows, но основная часть задач решается гораздо проще, если работать с цифрами числа при помощи программирования.

Чтобы разбить число на цифры, необходимо использовать цикл while. Общая идея заключается в том, что с помощью остатка от деления на 10 мы получаем последнюю цифру числа, а потом делим его на 10 и так, пока в нём будет оставаться хотя бы одна цифра.

Java

import java.util.Scanner;

public class Example1 {
    public static void main(String[] args) {
        // создаём сканер
        Scanner scanner = new Scanner(System.in);
        // читаем число
        int i = scanner.nextInt();
        // номер читаемого разряда
        int r = 0;
        // пока есть хотя бы одна цифра в числе
        while (i > 0) {
            // получаем цифру младшего разряда
            int c = i % 10;
            // выводим разряд и соответствующую ему цифру
            System.out.println(r + ": " + c);
            // увеличиваем номер текущего разряда
            r++;
            // отбрасываем младший разряд числа
            i /= 10;
        }

    }
}

C++

#include <iostream>

// главный метод программы
int main() {
    // читаем число
    int i;
    std::cin >> i;
    // номер читаемого разряда
    int r = 0;
    // пока есть хотя бы одна цифра в числе
    while (i > 0) {
        // получаем цифру младшего разряда
        int c = i % 10;
        std::cout << r << ": " << c << std::endl;
        // увеличиваем номер текущего разряда
        r++;
        // отбрасываем младший разряд числа
        i /= 10;
    }
    return 0;
}

Python

# читаем число
i = int(input())
# номер читаемого разряда
r = 0
# пока есть хотя бы одна цифра в числе
while i > 0:
    # получаем цифру младшего разряда
    c = i % 10
    # выводим разряд и соответствующую ему цифру
    print(r, ": ", c)
    # увеличиваем номер текущего разряда
    r = r + 1
    # отбрасываем младший разряд числа
    i = i // 10

Введём

5988701

Получим:

0: 1
1: 0
2: 7
3: 8
4: 8
5: 9
6: 5

В первом примере мы просто вывели номер разряда и цифру, которая стоит в нём. Если у вас не получается придумать, как перестроить этот цикл под ваши нужды, можно просто создать массив на основе этих цифр и работать уже с ним.

Java

import java.util.Scanner;

public class Example2 {
    public static void main(String[] args) {
        // создаём сканер
        Scanner scanner = new Scanner(System.in);
        // читаем число
        int n = scanner.nextInt();
        // инициализируем переменную цикла
        int i = n;
        // номер читаемого разряда
        int r = 0;
        // пока есть хотя бы одна цифра в числе
        while (i > 0) {
            // увеличиваем номер текущего разряда
            r++;
            // отбрасываем младший разряд числа
            i /= 10;
        }

        // создаём массив цифр по кол-ву разрядов
        int[] d = new int[r];
        // инициализируем переменную цикла
        i = n;
        // номер читаемого разряда
        r = 0;
        // пока есть хотя бы одна цифра в числе
        while (i > 0) {
            // получаем цифру младшего разряда
            d[r] = i % 10;
            // увеличиваем номер текущего разряда
            r++;
            // отбрасываем младший разряд числа
            i /= 10;
        }

        // Теперь можно работать с цифрами числа, как с массивом
        // для демонстрации эта программа просто выведет их в строчку
        // если идти по массиву от первого элемента к последнему, то
        // число выведется в развёрнутом виде. Ведь нулевой элемент
        // массива соответствует нулевому разряду числа, первый - первому и т.д.
        // поэтому массив следует вывести в обратном порядке
        for (int j = d.length - 1; j >= 0; j--) {
            System.out.print(d[j] + " ");
        }
        // перехожим на новую строку
        System.out.println();
    }
}

C++

#include <iostream>


// главный метод программы
int main() {
    // читаем число
    int n;
    std::cin >> n;
    // инициализируем переменную цикла
    int i = n;
    // номер читаемого разряда
    int r = 0;
    // пока есть хотя бы одна цифра в числе
    while (i > 0) {
        // увеличиваем номер текущего разряда
        r++;
        // отбрасываем младший разряд числа
        i /= 10;
    }

    // сохраняем кол-во разрядов
    int cnt = r;
    // создаём массив цифр по кол-ву разрядов
    int d[cnt];
    // инициализируем переменную цикла
    i = n;
    // номер читаемого разряда
    r = 0;
    // пока есть хотя бы одна цифра в числе
    while (i > 0) {
        // получаем цифру младшего разряда
        d[r] = i % 10;
        // увеличиваем номер текущего разряда
        r++;
        // отбрасываем младший разряд числа
        i /= 10;
    }

    // Теперь можно работать с цифрами числа, как с массивом
    // для демонстрации эта программа просто выведет их в строчку
    // если идти по массиву от первого элемента к последнему, то
    // число выведется в развёрнутом виде. Ведь нулевой элемент
    // массива соответствует нулевому разряду числа, первый - первому и т.д.
    // поэтому массив следует вывести в обратном порядке
    for (int j = cnt - 1; j >= 0; j--) {
        std::cout << d[j] << " ";
    }
    // перехожим на новую строку
    std::cout << std::endl;

    return 0;
}

Python

# читаем число
i = int(input())
# номер читаемого разряда
r = 0
# создаём список цифр
d = list()

# пока есть хотя бы одна цифра в числе
while i > 0:
    d.append(i % 10)
    # увеличиваем номер текущего разряда
    r = r + 1
    # отбрасываем младший разряд числа
    i = i // 10

# Теперь можно работать с цифрами числа, как с массивом
# для демонстрации эта программа просто выведет их в строчку
# если идти по массиву от первого элемента к последнему, то
# число выведется в развёрнутом виде. Ведь нулевой элемент
# массива соответствует нулевому разряду числа, первый - первому и т.д.
# поэтому массив следует вывести в обратном порядке
res_s = ""
for i in range(len(d)):
    res_s = res_s + str(d[len(d) - 1 - i]) + " "

# выводим строку
print(res_s)

Введём

5033891

Получим

5 0 3 3 8 9 1