Теория
Первая задача основана на теории графов. Для понимания хода решения нужно разобрать несколько связанных с ней вопросов.
Множество
Главным понятием теории графов является множество. Обычно это понятие принимается без определения. О множестве говорят, что оно просто содержит объекты, а про объекты вообще ничего не скажешь, кроме того, что они содержатся в множестве.
Это простейший способ построения научного основания. Мы замыкаем два понятия друг на друга, из этого появляется научный смысл: прочное, независимое основание. Уже имея основной смысл разрабатываемой теории, можно выполнять последующие построения. Такой подход использовал Гегель в своих построениях научной философии.
Спустя много лет Хайдеггер пошёл дальше и вывел, что смысл может быть построен не только на двух качественно противоположных понятиях (множество-объект, бытие-ничто и тд), но и от произвольного числа понятий, необязательно противоположных. Главное, чтобы они образовывали логический цикл и уточняли друг друга с каждым витком мысли. Если основание науки Гегеля сравнивать с двумерным ортонормированным базисом, то наука Хайдеггера - произвольный n-мерный.

Этот поход называется искусственно-научным. Следуя ему, мы сначала что-то придумываем, а потом ищем похожее в окружающем нас мире.
Второй подход - естественно-научный. Он обязывает нас все наши основополагающие понятия замыкать не только друг на друга, но и на восприятие окружающего мира, на взаимодействие с ним посредством эксперимента.
Главное основание естественно-научного подхода - это мысленное выведение. Повторив эксперимент несколько раз, мы верим, что последующие пройдут примерно также. Поэтому мы их не проводим, мы выводим общую закономерность, а через неё сможем мысленно представить ход любого схожего эксперимента. Это мысленное выведение выступает основанием, первичным смыслом для всех последующих мысленных выведений.
На нём основан, например, метод математической индукции. Только вместо экспериментов с окружающим миром мы исследуем поведение чисел и других искусственных понятий, не имеющих прямого отношения к окружающему нас миру и нашему восприятию. Следуя методу математической индукции, мы сначала выделяем основание, начало, первичный смысл, то, с чем невозможно поспорить. После этого мы доказываем индукционный переход, то самое мысленное выведение, индукция в широком смысле.
При помощи мысленного выведения мы можем порождать не только мысленные эксперименты или доказательства тождеств, но и выводить, например, сами числа. Натуральные числа 1,2,3 и тд порождены именно мысленным выведением. Каждое из чисел мы не усваивали за счёт восприятия окружающего мира. Мы узнали несколько основных чисел (через непосредственный опыт) и правила выведения остальных.
Мысленное выведение может работать и с настоящими предметами, людьми. Например, мы можем вывести понятие класс, как объединение учеников, состоящих в нём. Т. е. при определении класса мы явно перечисляем его учащихся. Роль мысленного выведения здесь выполняет перечисление. Таким образом, с точки зрения естественно-научного подхода:
Множество - это любой результат мысленного выведения, а объект - это образ, полученный на любом из шагов этого выведения.
Графы
На множестве могут быть определены не только сами объекты, но и отношения между ними. Например, на множестве натуральных чисел можно определить операцию сложения. Т.е. мы определяем правило, согласно которому двум объектам множества будем сопоставлять третий.
Граф - это множество с предельно простыми отношениями - отношениями связи. Объекты в графах называются вершинами. Т.е. о вершинах графа мы можем судить только с точки зрения их связности (совокупности связей с другими вершинами). Связи в графах называются рёбрами. Граф изображают в виде жирных точек(вершин) и соединяющих эти точки отрезков(рёбер)
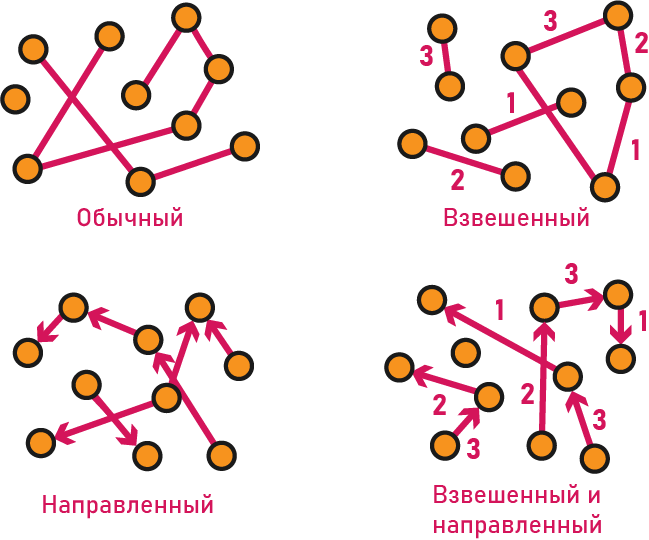
Связи бывают и более сложными, но для данного задания нам надо знать только два типа. Первый - это численные связи(каждому ребру сопоставляется число, вес). Граф с такими связями называется взвешенным, потому что каждому ребру сопоставляется свой вес. Второй тип - это направление связи. Направленная связь, направленное ребро означает, что при её описании важен порядок связи. "А связано с Б" в общем случае никак не зависит от "Б связано с А". Например, я могу видеть человека, а он не будет видеть меня, потому что стоит ко мне спиной. Граф может быть одновременно и взвешенным, и направленным. Это - независимые характеристики.
Взвешенный граф изображают так же, как обычный, но дополнительно рядом с каждым ребром пишут его вес(меру связи). Направление связи показывают за счёт того, что заменяют отрезок стрелочкой.
Связи графа можно показать не только рисуя вершины и рёбра. Для этого ещё используют таблицы.
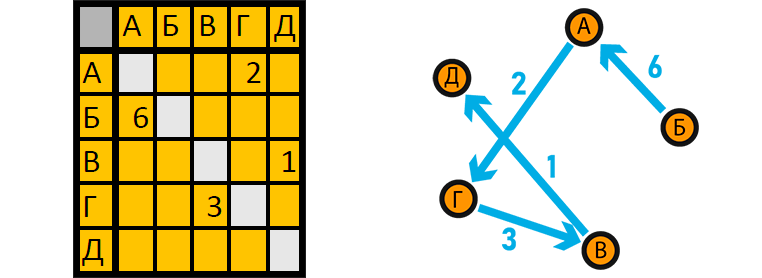
Таблица позволяет указать не просто наличие связи, но и её вес с направлением. Строка таблицы соответствует вершине, из которой исходит связь, а столбец - вершине, в которую связь входит. В клетке записывается вес ребра графа, его мера связи. Сама таблица называется матрицей смежности или весовой матрицей. Белые ячейки таблицы - это главная диагональ весовой матрицы, она отвечает за меру связи объекта с самим собой. В рамках ЕГЭшных задач мы считаем, что вершина не может быть связана сама с собой. Но в теории графов это, конечно же, не так.
Если связь двунаправленная, то элементы матрицы, симметричные относительно главной диагонали должны совпадать. Например, мера связи А с Б должна быть равна мере связи Б с А.
У каждой вершины можно определить количественную характеристику степень. Степень вершины - это величина, равная кол-ву рёбер, которыми соединена рассматриваемая вершина. Также можно определить взвешенную степень. Она равна сумме весов рёбер, соединённых с рассматриваемой вершиной.
На рисунке степени вершин обозначены фиолетовым, а взвешенные степени - зелёным.
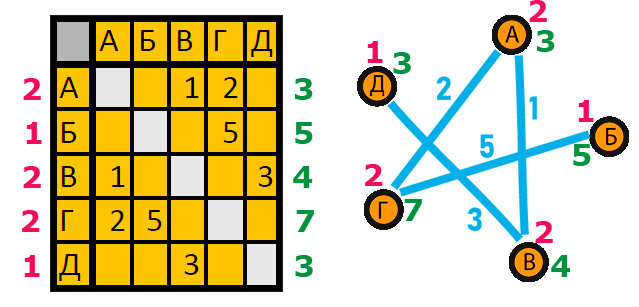
Если граф направленный, то определение степени вершины берётся таким, чтобы с ним было удобно работать в конкретной задаче. В обычном графе степень вершины можно найти, как количество непустых ячеек в строке таблицы, соответствующей рассматриваемой вершине. А взвешенную степень можно найти как сумму чисел, стоящих в ячейках рассматриваемой строки.