Задание 7

Изображения

Изображения на компьютере хранятся с помощью пикселей.

Количество пикселей изображения $N$ вычисляется как произведение ширины рисунка на высоту (в пикселях)

Для хранения растрового изображения нужно выделить в памяти

$$I = N * i$$

битов, где $N$ – количество пикселей и $i$ – глубина цвета (глубина кодирования, сколько бит отведено на один пиксель)

глубина кодирования – это количество бит, которые выделяются на хранение цвета одного пикселя

при глубине кодирования $i$ битов на пиксель код каждого пикселя выбирается из $2^i$ возможных вариантов, поэтому можно использовать не более $2^i$ различных цветов

DPI - это аббревиатура от «Dots Per Inch» и означает количество точек (пикселей) на дюйм (разрешение изображения). Дюйм - единица длины равная 2,541 см.

Пример 1

Задача

Для хранения в информационной системе документы сканируются с разрешением 200 dpi и цветовой системой, содержащей $130$ цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 10 Мбайт.

Для повышения качества представления информации было решено перейти на разрешение $300$ dpi и цветовую систему, содержащую $2^{16}$ = $65~536$ цветов.

Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?

Разрешение изображения изменилось с $200$ dpi на $300$ dpi. Это означает, что размер изображения изменился в $\frac{300* 300}{200 * 200} = \frac{9}{4}$ раз.

Для хранения цветовой системы, состоящей из 130 цветов, необходимо 8 бит (необходимо подобрать минимально возможный $i$, так, чтобы $N \leq 2^i; 130 \leq 2^8$).

Глубина кодирования изображения изменилась с $8$ бит до $16$ бит. Это означает, что размер изображения изменился в $\frac{16}{8} = 2$ раза.

Средний размер документа, отсканированного с изменёнными параметрами равно

$$10 * \frac{9}{4} * 2 = 45 Мбайт$$

Ответ: 45

Пример 2

Задача

Для хранения произвольного растрового изображения размером $128×320$ пикселей отведено $20 Кбайт$ памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?

находим количество пикселей, используя для вычисления степени числа $2$:

$$N = 128 * 320 = 2^7 * 2^5 * 10 = 2^{13} · 5$$

объём файла переводим из $Кбайт$ в биты

$$20 Кбайт = 20 · 2^{13} бит$$

глубина кодирования (количество битов, выделяемых на 1 пиксель):

$$\frac{20 * 2^{13}}{5 · 2^{13}} = 4 бит/пиксель$$

максимальное возможное количество цветов $2^4 = 16$

Ответ: 16

Пример 3

Задача

Рисунок размером 512 на 256 пикселей занимает в памяти 64 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.

находим количество пикселей, используя для вычисления степени числа $2$:

$$N = 512 * 256 = 2^9 * 2^8 = 2^{17}$$

объём файла в $Кбайтах$ $64 = 2^6$

объём файла в битах $2^6 * 2^{13} = 2^{19}$

глубина кодирования (количество битов, выделяемых на 1 пиксель): $219 / 217 = 2^2 = 4 бит/пиксель$

максимальное возможное количество цветов $2^4 = 16$

Ответ: 16

Пример 4

Задача

Какой минимальный объём памяти (в $Кбайт$) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером $64$ на $64$ пикселов при условии, что в изображении могут использоваться $256$ различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

находим количество пикселей, используя для вычисления степени числа $2$:

$$N = 64 * 64 = 2^6 * 2^6 = 2^{12}$$

$256 = 2^8$, поэтому для кодирования одного из $256$ вариантов цвета нужно выделить в памяти

$8 = 2^3 бит/пиксель$

объём файла в битах $2^{12} * 2^3 = 2^{15}

объём файла в Кбайтах

$$2^{15} / 2^{13} = 2^2 = 4$$

Ответ: 4

Звукозаписи

Для записи звука на компьютер специальная плата АЦП(аналогово-цифровой преобразователь) заданное количество раз в секунду измеряет уровень сигнала и преобразовывает его в число.

Кол-во измерений в секунду называется частотой дискретизации, измеряется в герцах(гц).

Кол-во бит, необходимое для определения цифрового сигнала из аналогового называется глубиной кодирования или разрешением. Чем больше бит занимает каждый замер звука, тем качественнее он звучит, переходы между звуками получаются более плавными.

Если запись ведётся в режиме моно, то записывается один канал, если в - стерео, то запись ведётся по двум каналам. Во втором случае количество информации следует умножать на два, т.к. каналы независимы.

Пример 5

Задача

Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 30 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось.

Полученный файл был передан в город Б; пропускная способность канала связи с городом Б в 4 раза выше, чем канала связи с городом А.

Сколько секунд длилась передача файла в город Б? В ответе запишите только целое число, единицу измерения писать не нужно.

Объём музыкального файла вычисляется по формуле $I=f*r*k*t$, где $f$ – частота дискретизации, $r$ – разрешение (глубина кодирования), $k$ – количество каналов, $t$ – время звучания.

При повышении разрешения (количества битов на хранения одного отсчёта) в $2$ раза объём файла (при прочих равных условиях) увеличивается в $2$ раза, поэтому время тоже увеличится в $2$ раза

При снижении частоты дискретизации (количества хранимых отсчётов за 1 секунду) в $1.5$ раза объём файла (при прочих равных условиях) уменьшается в $1.5$ раза, поэтому время тоже уменьшится в $1.5$ раза

При увеличении пропускной способности канала связи (здесь это то же самое, что и скорость передачи данных) в $4$ раза время передачи (при прочих равных условиях) уменьшится в $4$ раза

Поэтому исходное время передачи файла нужно

а) умножить на 2

б) разделить на 1,5

в) разделить на 4

Получается

$$30 * 2 / 1.5 / 4 = 10 с$$

Ответ: 10

Пример 6

Задача

Производилась двухканальная (стерео) звукозапись с частотой дискретизации $64 кГц$ и $24$-битным разрешением. В результате был получен файл размером $120$ Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) производилась запись. В качестве ответа укажите ближайшее к времени записи целое число, кратное $5$.

так как частота дискретизации $64 кГц$, за одну секунду запоминается 64000 значений сигнала

так как глубина кодирования – $24 бита = 3 байта$, для хранения $1$ секунды записи требуется

$$2 * 64000 * 3 байта$$

(коэффициент 2 – для стерео записи)

на $1 минуту = 60 секунд$ записи потребуется

$$60 * 2 * 64000 * 3 байта$$

Теперь разделим общий размер файла на вес одной минуты в бийтах:

$$t = \frac{120*1024*1024}{60 * 2 * 64000 * 3}$$

Вычислим значения этого выражения на калькуляторе, получим:

$$t = \frac{125829120}{23040000} \approx 5.46$$

Ближайшее целое число, кратное пяти - это и есть пять.

Ответ: 5

Пример 7

Задача

Производится одноканальная (моно) звукозапись с частотой дискретизации $64Гц$. При записи использовались $32$ уровня дискретизации. Запись длится $4 минуты 16 секунд$, её результаты записываются в файл, причём каждый сигнал кодируется минимально возможным и одинаковым количеством битов. Какое из приведённых ниже чисел наиболее близко к размеру полученного файла, выраженному в килобайтах?

1) 10

2) 64

3) 80

4) 512

Так как частота дискретизации 64 Гц, то за одну секунду запоминается 64 значения сигнала

Т.к. глубина кодирования не задана, необходимо вычислить её по количеству битов на один отсчёт(замер).

используется $32 = 2^5$ уровня дискретизации значения сигнала, поэтому на один отсчет приходится 5 бит

время записи $4 мин 16 с = 4 * 60 + 16 = 256 с$

за это время нужно сохранить

$$256 * 5 * 64 бит = 256 * 5 * 8 байт = 5 * 2 Кбайт = 10 Кбайт$$

Ответ: 1

Задания для самостоятельного выполнения

Передача данных

В этих задачах используется понятие сжатия данных. Сжатие - это особые операции над файлами, которые позволяют уменьшить их размер без потери информации.

Пример 8

Задача

Документ объёмом 40 Мбайт можно передать с одного компьютера на другой двумя способами.

А. Сжать архиватором, передать архив по каналу связи, распаковать.

Б. Передать по каналу связи без использования архиватора.

Какой способ быстрее и насколько, если:

• средняя скорость передачи данных по каналу связи составляет 223 бит в секунду;
• объём сжатого архиватором документа равен 90% исходного;
• время, требуемое на сжатие документа, – 16 секунд, на распаковку – 2 секунды?

В ответе напишите букву А, если быстрее способ А, или Б, если быстрее способ Б. Сразу после буквы напишите число, обозначающее, на сколько секунд один способ быстрее другого?

вспомним, что $1 Мбайт = 210 Кбайт = 220 байт = 223 бит$

время передачи несжатого файла (по варианту Б): $40 * 223 / 223 = 40 с$

время передачи файла по варианту А: $16 + 0.9 * 40 + 2 = 18 + 36 = 54 с$

таким образом, быстрее вариант Б на $54 – 40 = 14 с$

Ответ: Б14

Пример 8

Задача

Документ (без упаковки) можно передать по каналу связи с одного компьютера на другой за $75$ секунд. Если предварительно упаковать документ архиватором, передать упакованный документ, а потом распаковать на компьютере получателя, то общее время передачи (включая упаковку и распаковку) составит $30 секунд$. При этом на упаковку и распаковку данных всего ушло $15$ секунд. Размер исходного документа $20 Мбайт$. Чему равен размер упакованного документа (в Мбайт)?.

определяем скорость передачи данных по каналу связи:

$$q = 20 Мбайт / 75 c$$

тогда время передачи упакованного файла размером $x~Мбайт$ равно

$$x~Мбайт / v = x~Мбайт / (20~Мбайт / 75 c) = (75 * x / 20) с$$

по условию это время равно $30 – 15 = 15 с$

решаем уравнение $(75 * x / 20) с = 15 с$, получаем $x = 4 Мбайт$

Ответ: 4

Пример 9

Задача

Скорость передачи данных через ADSL-соединение равна $128000 бит/c$. Через данное соединение передают файл размером $625 Кбайт$. Определите время передачи файла в секундах.

Разложим заданные числа на удобные множители и переведем размер файла в биты, чтобы «согласовать» единицы измерения:

$$q =128000 бит/c = 128 * 1000 бит/с = 2^7 * 125 * 8 бит/с = 2^7 * 5^3 * 2^3 бит/с = 2^{10} * 5^3 бит/с$$

$$Q =625 Кбайт = 5^4 Кбайт = 5^4 · 2^{13} бит$$

чтобы найти время передачи в секундах, нужно разделить размер файла на скорость передачи:

$$t \frac{Q}{q}=\frac{5^4 · 2^{13} }{2^{10} * 5^3}=5*2^3с=40с$$

Ответ: 40с

Пример 9

Задача

У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 256 Кбит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 32 Кбит в секунду.

Петя договорился с Васей, что тот будет скачивать для него данные объемом 5 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу.

Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 512 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.

Сначала нарисуем схему:

Фактически нужно определить, сколько времени будет передаваться файл объемом 5 Мбайт по каналу со скоростью передачи данные 32 Кбит/с; к этому времени нужно добавить задержку файла у Васи (пока он не получит 512 Кбайт данных по каналу со скоростью 256 Кбит/с);

Можно построить диаграмму, где на горизонтальной оси откладывается время:

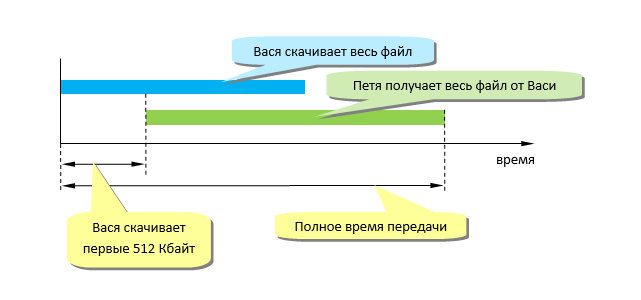
Такие диаграммы называются диаграммами Ганта

Согласовываем единицы измерения, находим объем файла в Кбитах:

$$Q = 5*2^{10}Кбайт = 5*2^{13}Кбит$$

время «чистой» передачи файла от Васи к Пете со скоростью $q=32 Кбит/с$

$$t = \frac{Q}{q} = \frac{5*2^{13}}{32}=5*256 = 1280c$$

определяем, сколько Кбит должен скачать Вася до начала передачи Пете:

$$Q_0 = 512Кбайт=512*8$$

Задержка файла у Васи = время скачивания файла объемом $512 Кбайт$ со скоростью $q_0=256 Кбит/с$

$$t_0 = \frac{Q_0}{q_0} = \frac{512*8}{256}=16с$$

общее время

$$T = t + t_0 = 16+1280=1296c$$

Ответ: 1296c

Задания для самостоятельного выполнения