Задание 9

для вычисления максимального, минимального и среднего арифметического значений диапазона (например, A1:G20) используются соответственно функции

Максимум диапазона	MAX(A1:G20)	МАКС(A1:G20)
Минимум диапазона	MIN(A1:G20)	МИН(A1:G20)
Среднее значение диапазона	AVERAGE(A1:G20)	СРЗНАЧ(A1:G20)

Слева записаны английские названия, справа – русские (выбор зависит от программы и версии операционной системы).

в списке аргументов этих функций можно указывать несколько диапазонов и адресов ячеек, разделив их точкой с запятой, например:

МАКС(A1:G20;H15;K12:Y90)

МИН(A1:G20;H15;K12:Y90)

СРЗНАЧ(A1:G20;H15;K12:Y90)

все три функции игнорируют (не учитывают) пустые ячейки и ячейки, содержащие нечисловые (например, текстовые) данные; например

Пример 1

Задача 1

Откройте файл электронной таблицы 9-0.xls, содержащей вещественные числа – результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Найдите разность между максимальным значением температуры и её средним арифметическим значением. В ответе запишите только целую часть получившегося числа.

откроем электронную таблицу (на рисунке показан её левый верхний угол):

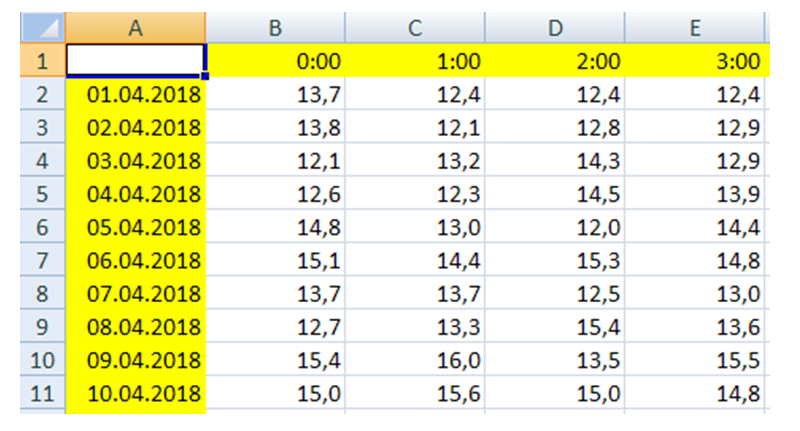
первый вопрос, который нужно решить – куда записать формулу; для этого нужно использовать ПУСТУЮ ячейку, в данном случае очень удобно выбрать ячейку А1

далее выясняем, в каком диапазоне находятся данные (без заголовков строк и столбцов, которые на рисунке выделены жёлтым фоном); левый верхний угол – это ячейка B2, а правый нижний – Y92:

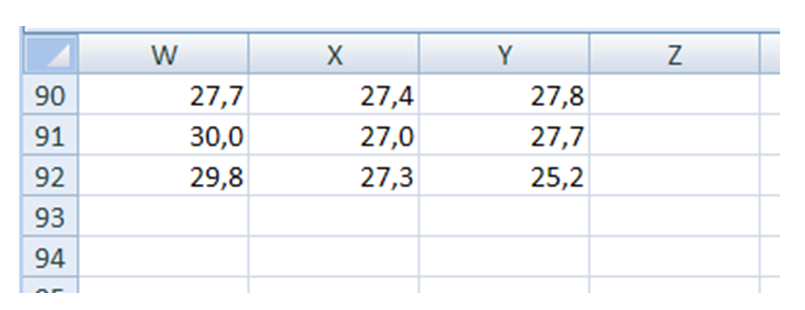
так что получается диапазон $B2:Y92$

вписываем в ячейку A1 формулу

=МАКС(B2:Y92)-СРЗНАЧ(B2:Y92)

после ввода формулы получаем значение 14.3, из которого нужно выделить целую часть (НЕ ОКРУГЛИТЬ!, например для значения 14,9 ответ также будет 14)

Ответ: 14

Обратите внимание

В этом задании требуется не округлить полученное значение, а записать его целую часть. Для этого вам нужно в электронных таблицах найти результат с достаточно большим количеством знаков в дробной части.

Когда можно ошибиться? «Под подозрение» попадают результаты, где в дробной части получаются нули. Предположим, что вы установили формат с одним знаком после запятой и получили результат 10,0. Значит ли это, что ответ к задаче – 10? К сожалению, нет, ведь табличный процессор округляет результат до нужного количества знаков. Поэтому возможно, что округлённое число равно 9,96, и в этом случае правильный ответ – 9.

Хватит ли трёх знаков в дробной части? Не факт. Ведь может быть, что вы увидели на экране число 10,000, а «под ним» скрывается число 9,9996. Поэтому нужно устанавливать столько знаков в дробной части, чтобы хотя бы одна цифра после занятой была ненулевая.

Задания для самостоятельного выполнения

Таблицы для заданий

Пример 2

Задача

Дан фрагмент электронной таблицы:

Какое целое число должно быть записано в ячейке A1, чтобы диаграмма, построенная по значениям ячеек диапазона A2:D2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона A1:D1 – целые и положительные.

сначала предполагаем, что диаграмма не повернута, то есть первый сектор начинается с направления «на север» (вверх от центра)

по диаграмме определяем, что третий и четвёртый сектора в два раза больше остальных двух, то есть $A2 = B2 = C2/2 = D2 / 2$

обозначив значение $A1$ за $x$, записываем значения ячеек второй строки:

$$A2=B2=4-x,~C2=D2=2(4-x)=8-2x=4+D1$$

решаем последнее уравнение относительно $D1$:

$$8-2x = 4+D1\\ d1=4-2x$$

поскольку по условию $D1$ – целое и больше нуля, единственное подходящее целое значение x > 0 $ равно $1 ($x\leq 0$ не может быть по условию, при целых $x > 1$ получаем $D1 \leq 0$, что тоже невозможно по условию)

Ответ: 1

Пример 3

Задача

Дан фрагмент электронной таблицы:

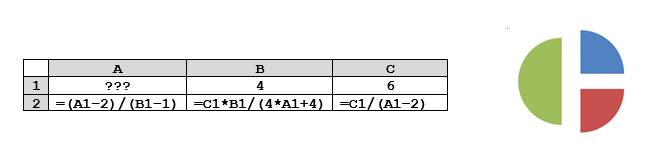
Какое целое число должно быть записано в ячейке A1, чтобы диаграмма, построенная по значениям ячеек диапазона A2:С2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.

Сначала предполагаем, что диаграмма не повернута, то есть первый сектор начинается с направления «на север» (вверх от центра)

По диаграмме определяем, что третий сектор в два раза больше остальных двух, то есть $A2 = B2 = C2/2$

Обозначив значение $A1$ за $x$, записываем значения ячеек второй строки:

$A2=\frac{x-2}{3},~B2=\frac{24}{4x+4}=\frac{6}{x+1}, C2=\frac{6}{x-2}

Чтобы найти $x$, можно решить одно из трёх уравнений: $A2 = B2, B2 = C2/2, A2 = C2/2$

Причём проще решать уравнение $B2=C2/2$, поскольку оно линейное, а остальные два сводятся к квадратным уравнениям

Решим уравнение $B2 = C2/2$:

$$\frac{6}{x+1}=\frac{6}{2(x-2)}\Rightarrow~x+1=2x-4\Rightarrow x=5$$

6) проверяем условие A2=B2 при x = 5:

$$\frac{5-2}{3}=1=\frac{6}{2(x-2)}$$

Всё верно

Ответ: 5.

Пример 4

Задача

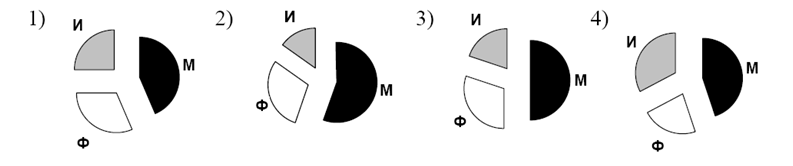
На диаграмме показано количество призеров олимпиады по информатике (И), математике (М), физике (Ф) в трех городах России.

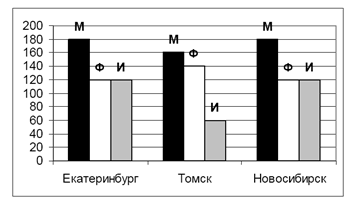
Какая из диаграмм правильно отражает соотношение общего числа призеров по каждому предмету для всех городов вместе?

В условии дана столбчатая диаграмма, по которой можно определить все числовые данные

В ответах все диаграммы – круговые, по ним можно определить только доли отдельных составляющих в общей сумме

При анализе диаграмм-ответов нужно «вылавливать» их характерные черты (половину или четверть круга, одинаковые значения, соотношения между секторами), именно они позволяют определить верный ответ

Попробуем сначала проанализировать круговые диаграммы (ответы)

• наибольшая доля (на всех диаграммах) приходится на математику
• самый меньший сектор на диаграммах 1-3 – информатика, а на 4-ой – физика
• на 1-ой диаграмме информатика составляет четверть от общей суммы
• на 3-ей диаграмме математика составляет половину от общей суммы

Теперь снимем данные с заданной столбчатой диаграммы и подсчитаем сумму призеров по каждому предмету:

По условию для построения круговой диаграммы использовалась нижняя строка таблицы

Общее количество призеров ¬ – 1200, информатика составляет ровно четверть от этого числа

Таким образом, правильный ответ – 1.

Ответ: 1.

Пример 5

Задача

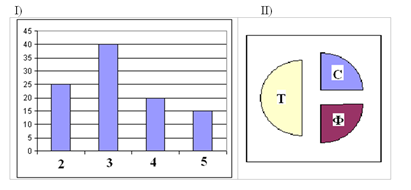
В цехе трудятся рабочие трех специальностей – токари (Т), слесари (С) и фрезеровщики (Ф). Каждый рабочий имеет разряд не меньший второго и не больший пятого. На диаграмме I отражено количество рабочих с различными разрядами, а на диаграмме II – распределение рабочих по специальностям. Каждый рабочий имеет только одну специальность и один разряд

Имеются четыре утверждения:

А) Все рабочие третьего разряда могут быть токарями

Б) Все рабочие третьего разряда могут быть фрезеровщиками

В) Все слесари могут быть пятого разряда

Г) Все токари могут быть четвертого разряда

Какое из этих утверждений следует из анализа обеих диаграмм?

1) А

2) Б

3) В

4) Г

В условии даны столбчатая диаграмма, по которой можно определить все числовые данные, и круговая диаграмма, по которой можно определить только доли отдельных составляющих в общей сумме

По данным столбчатой диаграммы определим, сколько рабочих имеют 2-ой, 3-й, 4-й и 5-й разряды:

2-ой разряд:	25 чел.	3-й разряд:	40 чел.
4-й разряд:	20 чел.	5-й разряд:	15 чел.

Сложив все эти числа, определим, что всего в цехе 25 + 40 + 20 + 15 = 100 рабочих

По круговой диаграмме видим, что половина из них – токари (значит их 50 человек), четверть – слесари (25 чел.) и еще четверть – фрезеровщики (25 чел.)

Теперь последовательно рассмотрим все утверждения-ответы:

А: Все рабочие третьего разряда (их 40 чел.) МОГУТ быть токарями, потому в цеху 50 токарей

Б: Все рабочие третьего разряда (их 40 чел.) НЕ могут быть фрезеровщиками, потому в цеху всего 25 фрезеровщиков

В: Все слесари (их 25 чел.) НЕ могут быть 5-ого разряда, потому в цеху только 15 рабочих имеют 5-й разряд

Г: Все токари (их 50 чел.) НЕ могут быть четвертого разряда, потому в цеху только 20 рабочих имеют 4-й разряд

Таким образом, правильный ответ – 1.

Ответ: 1.

Пример 6

Задача

Дан фрагмент электронной таблицы в режиме отображения формул.

После копирования диапазона ячеек АЗ:ЕЗ в диапазон А4:Е6 была построена диаграмма (график) по значениям столбцов диапазона ячеек В2:Е6.

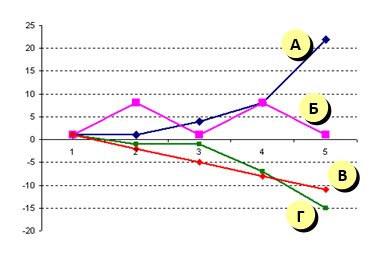
Значениям С2:С6 соответствует график

1) А

2) Б

3) В

4) Г

Прежде всего разберемся, что значит фраза «После копирования диапазона ячеек АЗ:ЕЗ в диапазон А4:Е6»; очевидно, что размеры диапазонов АЗ:ЕЗ и А4:Е6 разные, поэтому авторы задачи имели ввиду следующее: выделяется диапазон АЗ:ЕЗ и «растягивается» вниз за маркер заполнения до строки 6:

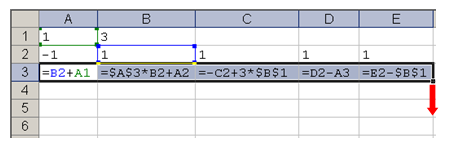
При этом формула, находящаяся в А3, скопируется в ячейки А4:А6, формула из В3 – в ячейки В4:В6 и т.д.

По условию нас в конечном счете интересует только столбец С, посмотрим, что получится при копировании формулы из С3 (=-C2+3*$B$1) в ячейки С4:С6

В этой формуле есть ссылки на две ячейки – одна относительная, на С2 (при копировании она будет меняться (на С3, С4 и т.д.), а вторая – абсолютная, на В1, она при копировании не изменится:

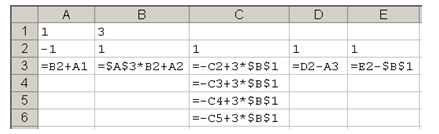
Видим, что формулы в столбце С зависят только от В1 и ячеек этого же столбца, поэтому не нужно рассчитывать все остальные ячейки

Последовательно найдем все числа в диапазоне С3:С6:

$С3=-С2+3*В1=-1+3*3=8$

$С4=-С3+3*В1=-8+3*3=1$

$С5=-С4+3*В1=-1+3*3=8$

$С6=-С5+3*В1=-8+3*3=1$

посмотрев на график, видим, что именно так меняются данные на графике Б

таким образом, правильный ответ – 2.

Ответ: 2.

Задания для самостоятельного выполнения