Skip to main content

Примеры

Здесь приведены задания и соответствующие им программы, все пояснения в коде.

Задания для самостоятельного выполнения

Пример 3​

Задание

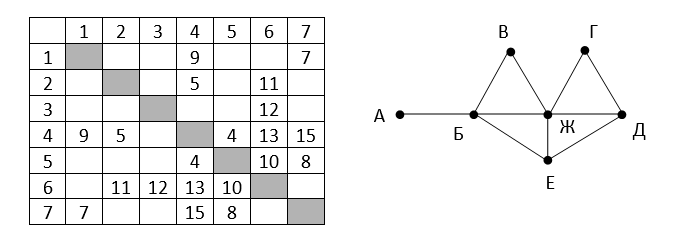
Р-10 (демо-2021). На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова протяжённость дороги из пункта Г в пункт Ж. В ответе запишите целое число – так, как оно указано в таблице. Задание 3

public class Example3 {

    // кол-во вершин (используется для удобства)
    static int SIZE = 7;

    // названия вершин
    static char[] names = {'А', 'Б', 'В', 'Г', 'Д', 'Е', 'Ж'};

    //      П1  П2  П3  П4  П5  П6  П7
    static int[][] source = new int[][]{
            {0, 0, 0, 9, 0, 0, 7}, // П1
            {0, 0, 0, 5, 0, 11, 0}, // П2
            {0, 0, 0, 0, 0, 12, 0}, // П3
            {9, 5, 0, 0, 4, 13, 15}, // П4
            {0, 0, 0, 4, 0, 10, 8}, // П5
            {0, 11, 12, 13, 10, 0, 0}, // П6
            {7, 0, 0, 15, 8, 0, 0}  // П7
    };
    //       А  Б  В  Г  Д  Е  Ж
    static int[][] target = new int[][]{
            {0, 1, 0, 0, 0, 0, 0}, // A
            {1, 0, 1, 0, 0, 1, 1}, // Б
            {0, 1, 0, 0, 0, 0, 1}, // В
            {0, 0, 0, 0, 1, 0, 1}, // Г
            {0, 0, 0, 1, 0, 1, 1}, // Д
            {0, 1, 0, 0, 1, 0, 1}, // Е
            {0, 1, 1, 1, 1, 1, 0}  // Ж
    };

    // степени вершин
    static int[] sourceSum = new int[SIZE];
    static int[] targetSum = new int[SIZE];

    // получить обратную перестановку
    static int[] getReversePermutation(int[] arr) {
        int[] reverse = new int[arr.length];
        for (int i = 0; i < SIZE; i++) {
            reverse[arr[i]] = i;
        }
        return reverse;
    }

    // обработка перестановки
    static void processPermutation(int[] arr) {
        // проверяем, что в представлениях совпадают степени вершин
        for (int i = 0; i < SIZE; i++) {
            if (sourceSum[arr[i]] != targetSum[i]) {
                return;
            }
        }

        // нужна проверка связности, т.е. того, что при перестановке все связи сохраняются, те не
        // обратятся в ноль
        for (int i = 0; i < SIZE; i++) {
            for (int j = 0; j < SIZE; j++) {
                // если в эталонном представлении связь между вершинами есть,
                // а в данном в задании - нет
                if (target[i][j] > 0 && source[arr[i]][arr[j]] == 0)
                    // заканчиваем выполнение обработчика, потому такая перестановка
                    // создаёт представление, не совместимое с данным, а значит, нас не
                    // интересует
                    return;
            }
        }
        // здесь мы уже выполняем проверку, определённую заданием

        // получаем обратную перестановку
        int[] reverse = getReversePermutation(arr);
        // выводим названия вершин
        for (int i = 0; i < SIZE; i++) {
            System.out.print(names[reverse[i]] + " ");
        }
        System.out.println();
        int gjDistance = source[arr[6]][arr[3]];
        System.out.println(gjDistance);


    }

    // поменять местами элементы массива arr с индексами l и r
    public static void swap(int[] arr, int l, int r) {
        int tmp = arr[l];
        arr[l] = arr[r];
        arr[r] = tmp;
    }


    // функция-генератор перестановок
    static void permute(int[] p, int pos) {
        // Если мы дошли до последнего элемента
        if (pos == SIZE - 1) {
            processPermutation(p);
        } else { // иначе
            // Перебираем все оставшиеся элементы
            for (int i = pos; i < SIZE; i++) {
                // меняем местами текущий элемент и перебираемый
                swap(p, pos, i);
                // Вызываем Рекурсию для следующего элемента
                permute(p, pos + 1);
                // меняем местами обратно
                swap(p, pos, i);
            }
        }
    }

    // главный метод программы
    public static void main(String[] args) {
        // рассчитываем взвешенные степени
        for (int i = 0; i < SIZE; i++) {
            sourceSum[i] = 0;
            targetSum[i] = 0;
            for (int j = 0; j < SIZE; j++) {
                // в исходном представлении надо не забыть заменить ненулевые веса единицей
                sourceSum[i] += Math.signum(source[i][j]);
                targetSum[i] += target[i][j];
            }
        }
        // запускаем генерацию перестановок
        permute(new int[7]{0, 1, 2, 3, 4, 5, 6}, 0);
    }

}

На выходе получим:

Г В А Ж Е Б Д
9

Пример 4​

Задание

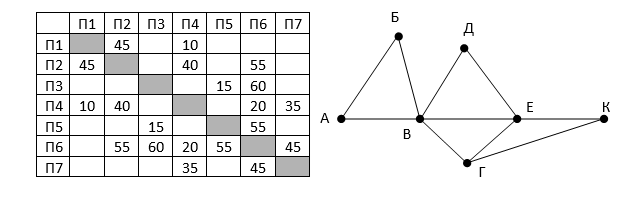
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Е. В ответе запишите целое число – так, как оно указано в таблице. Задание 4

public class Example4 {

    // кол-во вершин (используется для удобства)
    static int SIZE = 7;

    // названия вершин
    static char[] names = {'А', 'Б', 'В', 'Г', 'Д', 'Е', 'К'};

    //      П1  П2  П3  П4  П5  П6  П7
    static int[][] source = new int[][]{
            {0, 45, 0, 10, 0, 0, 0}, // П1
            {45, 0, 0, 40, 0, 55, 0}, // П2
            {0, 0, 0, 0,15, 60, 0}, // П3
            {10, 40, 0, 0, 0, 20, 35}, // П4
            {0, 0, 15, 0, 0, 55, 0}, // П5
            {0, 55, 60, 20, 55, 0, 45}, // П6
            {0, 0, 0, 35, 0, 45, 0}  // П7
    };
    //       А  Б  В  Г  Д  Е  К
    static int[][] target = new int[][]{
            {0, 1, 1, 0, 0, 0, 0}, // A
            {1, 0, 1, 0, 0, 0, 0}, // Б
            {1, 1, 0, 1, 1, 1, 0}, // В
            {0, 0, 1, 0, 0, 1, 1}, // Г
            {0, 0, 1, 0, 0, 1, 0}, // Д
            {0, 0, 1, 1, 1, 0, 1}, // Е
            {0, 0, 0, 1, 0, 1, 0}  // К
    };

    // степени вершин
    static int[] sourceSum = new int[SIZE];
    static int[] targetSum = new int[SIZE];

    // получить обратную перестановку
    static int[] getReversePermutation(int[] arr) {
        int[] reverse = new int[arr.length];
        for (int i = 0; i < SIZE; i++) {
            reverse[arr[i]] = i;
        }
        return reverse;
    }

    // обработка перестановки
    static void processPermutation(int[] arr) {
        // проверяем, что в представлениях совпадают степени вершин
        for (int i = 0; i < SIZE; i++) {
            if (sourceSum[arr[i]] != targetSum[i]) {
                return;
            }
        }

        // нужна проверка связности, т.е. того, что при перестановке все связи сохраняются, те не
        // обратятся в ноль
        for (int i = 0; i < SIZE; i++) {
            for (int j = 0; j < SIZE; j++) {
                // если в эталонном представлении связь между вершинами есть,
                // а в данном в задании - нет
                if (target[i][j] > 0 && source[arr[i]][arr[j]] == 0)
                    // заканчиваем выполнение обработчика, потому такая перестановка
                    // создаёт представление, не совместимое с данным, а значит, нас не
                    // интересует
                    return;
            }
        }
        // здесь мы уже выполняем проверку, определённую заданием

        // получаем обратную перестановку
        int[] reverse = getReversePermutation(arr);
        // выводим названия вершин
        for (int i = 0; i < SIZE; i++) {
            System.out.print(names[reverse[i]] + " ");
        }
        System.out.println();
        int veDistance = source[arr[2]][arr[5]];
        System.out.println(veDistance);

    }

    // поменять местами элементы массива arr с индексами l и r
    public static void swap(int[] arr, int l, int r) {
        int tmp = arr[l];
        arr[l] = arr[r];
        arr[r] = tmp;
    }


    // функция-генератор перестановок
    static void permute(int[] p, int pos) {
        // Если мы дошли до последнего элемента
        if (pos == SIZE - 1) {
            processPermutation(p);
        } else { // иначе
            // Перебираем все оставшиеся элементы
            for (int i = pos; i < SIZE; i++) {
                // меняем местами текущий элемент и перебираемый
                swap(p, pos, i);
                // Вызываем Рекурсию для следующего элемента
                permute(p, pos + 1);
                // меняем местами обратно
                swap(p, pos, i);
            }
        }
    }

    // главный метод программы
    public static void main(String[] args) {
        // рассчитываем взвешенные степени
        for (int i = 0; i < SIZE; i++) {
            sourceSum[i] = 0;
            targetSum[i] = 0;
            for (int j = 0; j < SIZE; j++) {
                // в исходном представлении надо не забыть заменить ненулевые веса единицей
                sourceSum[i] += Math.signum(source[i][j]);
                targetSum[i] += target[i][j];
            }
        }
        // запускаем генерацию перестановок
        permute(new int[]{0, 1, 2, 3, 4, 5, 6}, 0);
    }

}

На выходе получим:

К Г А Е Б В Д
20
К Г Б Е А В Д
20

Пример 5​

Задание

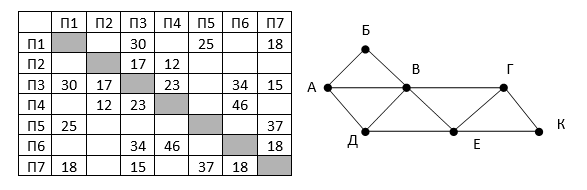
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта А в пункт Д. В ответе запишите целое число – так, как оно указано в таблице. Задание 5

public class Example5 {

    // кол-во вершин (используется для удобства)
    static int SIZE = 7;

    // названия вершин
    static char[] names = {'А', 'Б', 'В', 'Г', 'Д', 'Е', 'К'};

    //      П1  П2  П3  П4  П5  П6  П7
    static int[][] source = new int[][]{
            {0, 0, 30, 0, 25, 0, 18}, // П1
            {0, 0, 17, 12, 0, 0, 0}, // П2
            {30, 17, 0, 23,0, 34, 15}, // П3
            {0, 12, 23, 0, 0, 46, 0}, // П4
            {25, 0, 0, 0, 0, 0, 37}, // П5
            {0, 0, 34, 46, 0, 0, 18}, // П6
            {18, 0, 15, 0, 37, 18, 0}  // П7
    };
    //       А  Б  В  Г  Д  Е  К
    static int[][] target = new int[][]{
            {0, 1, 1, 0, 1, 0, 0}, // A
            {1, 0, 1, 0, 0, 0, 0}, // Б
            {1, 1, 0, 1, 1, 1, 0}, // В
            {0, 0, 1, 0, 0, 1, 1}, // Г
            {1, 0, 1, 0, 0, 1, 0}, // Д
            {0, 0, 1, 1, 1, 0, 1}, // Е
            {0, 0, 0, 1, 0, 1, 0}  // К
    };

    // степени вершин
    static int[] sourceSum = new int[SIZE];
    static int[] targetSum = new int[SIZE];

    // получить обратную перестановку
    static int[] getReversePermutation(int[] arr) {
        int[] reverse = new int[arr.length];
        for (int i = 0; i < SIZE; i++) {
            reverse[arr[i]] = i;
        }
        return reverse;
    }

    // обработка перестановки
    static void processPermutation(int[] arr) {
        // проверяем, что в представлениях совпадают степени вершин
        for (int i = 0; i < SIZE; i++) {
            if (sourceSum[arr[i]] != targetSum[i]) {
                return;
            }
        }

        // нужна проверка связности, т.е. того, что при перестановке все связи сохраняются, те не
        // обратятся в ноль
        for (int i = 0; i < SIZE; i++) {
            for (int j = 0; j < SIZE; j++) {
                // если в эталонном представлении связь между вершинами есть,
                // а в данном в задании - нет
                if (target[i][j] > 0 && source[arr[i]][arr[j]] == 0)
                    // заканчиваем выполнение обработчика, потому такая перестановка
                    // создаёт представление, не совместимое с данным, а значит, нас не
                    // интересует
                    return;
            }
        }
        // здесь мы уже выполняем проверку, определённую заданием

        // получаем обратную перестановку
        int[] reverse = getReversePermutation(arr);
        // выводим названия вершин
        for (int i = 0; i < SIZE; i++) {
            System.out.print(names[reverse[i]] + " ");
        }
        System.out.println();
        int adDistance = source[arr[0]][arr[4]];
        System.out.println(adDistance);

    }

    // поменять местами элементы массива arr с индексами l и r
    public static void swap(int[] arr, int l, int r) {
        int tmp = arr[l];
        arr[l] = arr[r];
        arr[r] = tmp;
    }


    // функция-генератор перестановок
    static void permute(int[] p, int pos) {
        // Если мы дошли до последнего элемента
        if (pos == SIZE - 1) {
            processPermutation(p);
        } else { // иначе
            // Перебираем все оставшиеся элементы
            for (int i = pos; i < SIZE; i++) {
                // меняем местами текущий элемент и перебираемый
                swap(p, pos, i);
                // Вызываем Рекурсию для следующего элемента
                permute(p, pos + 1);
                // меняем местами обратно
                swap(p, pos, i);
            }
        }
    }

    // главный метод программы
    public static void main(String[] args) {
        // рассчитываем взвешенные степени
        for (int i = 0; i < SIZE; i++) {
            sourceSum[i] = 0;
            targetSum[i] = 0;
            for (int j = 0; j < SIZE; j++) {
                // в исходном представлении надо не забыть заменить ненулевые веса единицей
                sourceSum[i] += Math.signum(source[i][j]);
                targetSum[i] += target[i][j];
            }
        }
        // запускаем генерацию перестановок
        permute(new int[]{0, 1, 2, 3, 4, 5, 6}, 0);
    }
}

На выходе получим:

Г Б В А К Д Е
46

Пример 6​

Задание

Р-04. Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)

Определите длину кратчайшего пути между пунктами A и G (при условии, что передвигаться можно только по построенным дорогам).

Задание 8

public class Example8 {
    // названия вершин
    static char[] names = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
    // кол-во вершин графа
    static int SIZE = 7;
    //       A  B  C  D  E  F G
    static int[][] m = new int[][]{
            {0, 5, 0, 12, 0, 0, 25}, // A
            {5, 0, 0, 8, 0, 0, 0}, // B
            {0, 0, 0, 2, 4, 5, 10}, // C
            {12, 8, 2, 0, 0, 0, 0}, // D
            {0, 0, 4, 0, 0, 0, 5}, // E
            {0, 0, 5, 0, 0, 0, 5}, // F
            {25, 0, 10, 0, 5, 5, 0}, // G
    };

    static int findMinDistance(int start, int end) {
        // заполняем расстояния от начальной вершины до рассматриваемой значениями -1
        int[] distances = new int[SIZE];
        Arrays.fill(distances,-1);
        // начинаем с точки Б, поэтому индекс 1
        int currentPoint = start;
        // расстояние от точки до самой себя равно нулю
        distances[currentPoint] = 0;
        // массив флагов, закончена ли проверка для заданной точки
        boolean[] complete = new boolean[SIZE];
        // пока есть следующая точка
        while (currentPoint != -1) {
            // перебираем все вершины
            for (int i = 0; i < SIZE; i++) {
                if (i == currentPoint || complete[i])
                    continue;
                // если у текущей есть с ней ребро
                if (m[currentPoint][i] > 0) {
                    // если мы не обрабатывали вершину или новое расстояние через рассматриваемую вершину выше
                    if (distances[i] == -1 || distances[i] > distances[currentPoint] + m[currentPoint][i]) {
                        // рассчитываем новое расстояние, как сумму длины пути до текущей вершины
                        // и ребра от текущей вершины до заданной
                        distances[i] = distances[currentPoint] + m[currentPoint][i];
                    }
                }
            }
            complete[currentPoint] = true;
            // ищем следующую точку
            int nextPoint = -1;
            for (int i = 0; i < SIZE; i++) {
                // если обработка точки не завершена
                if (!complete[i])
                    // если мы уже доходили до точки и следующая точка ещё не задана или
                    // новое расстояние меньше
                    if (distances[i] > 0 && (nextPoint == -1 || distances[i] < distances[nextPoint])) {
                        nextPoint = i;
                    }

            }
            // переходим к следующей точке
            currentPoint = nextPoint;
        }
        return distances[end];
    }

    public static void main(String[] args) {
        System.out.println(findMinDistance(0, 6));
    }
}

На выходе получим:

23

Пример 7​

Задание

Р-03. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)

Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам). Задание 8

public class Example9 {
    // названия вершин
    static char[] names = {'A', 'B', 'C', 'D', 'E', 'F'};
    // кол-во вершин графа
    static int SIZE = 6;
    //       A  B  C  D  E  F
    static int[][] m = new int[][]{
            {0, 2, 4, 0, 0, 0}, // A
            {2, 0, 1, 0, 7, 0}, // B
            {4, 1, 0, 3, 4, 0}, // C
            {0, 0, 3, 0, 3, 0}, // D
            {0, 7, 4, 3, 0, 2}, // E
            {0, 0, 0, 0, 2, 0}, // F
    };

    static int findMinDistance(int start, int end) {
        // заполняем расстояния от начальной вершины до рассматриваемой значениями -1
        int[] distances = new int[SIZE];
        Arrays.fill(distances,-1);
        // начинаем с точки Б, поэтому индекс 1
        int currentPoint = start;
        // расстояние от точки до самой себя равно нулю
        distances[currentPoint] = 0;
        // массив флагов, закончена ли проверка для заданной точки
        boolean[] complete = new boolean[SIZE];
        // пока есть следующая точка
        while (currentPoint != -1) {
            // перебираем все вершины
            for (int i = 0; i < SIZE; i++) {
                if (i == currentPoint || complete[i])
                    continue;
                // если у текущей есть с ней ребро
                if (m[currentPoint][i] > 0) {
                    // если мы не обрабатывали вершину или новое расстояние через рассматриваемую вершину выше
                    if (distances[i] == -1 || distances[i] > distances[currentPoint] + m[currentPoint][i]) {
                        // рассчитываем новое расстояние, как сумму длины пути до текущей вершины
                        // и ребра от текущей вершины до заданной
                        distances[i] = distances[currentPoint] + m[currentPoint][i];
                    }
                }
            }
            complete[currentPoint] = true;
            // ищем следующую точку
            int nextPoint = -1;
            for (int i = 0; i < SIZE; i++) {
                // если обработка точки не завершена
                if (!complete[i])
                    // если мы уже доходили до точки и следующая точка ещё не задана или
                    // новое расстояние меньше
                    if (distances[i] > 0 && (nextPoint == -1 || distances[i] < distances[nextPoint])) {
                        nextPoint = i;
                    }

            }
            // переходим к следующей точке
            currentPoint = nextPoint;
        }
        return distances[end];
    }

    public static void main(String[] args) {
        System.out.println(findMinDistance(0, 5));
    }
}

На выходе получим:

9