Дополнительно
Есть ещё несколько типов задач, которые встречаются редко, но всё равно стоит их разобрать. Решать их проще вручную, а не с использованием программирования. Объяснения этого блока взяты у Полякова
Аэропорты
Общая идея таких задач заключается в том, что нам нужно по расписанию вылетов проложить маршрут.
Р-02. Между четырьмя местными аэропортами: ОКТЯБРЬ, БЕРЕГ, КРАСНЫЙ и СОСНОВО, ежедневно выполняются
авиарейсы. Приведён фрагмент расписания перелётов между ними:
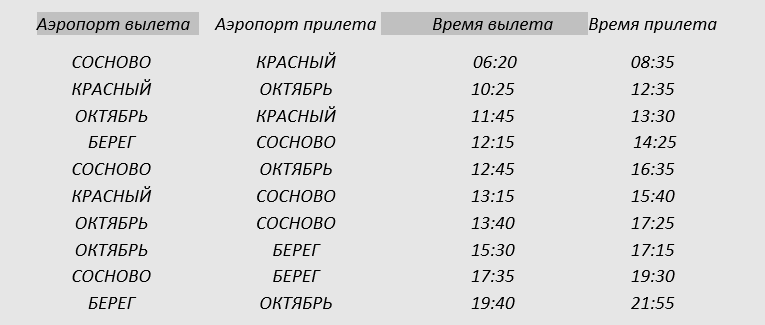Путешественник оказался в аэропорту ОКТЯБРЬ в полночь (0:00). Определите самое раннее время,
когда он может попасть в аэропорт СОСНОВО.
1) 15:40 2) 16:35 3) 17:15 4) 17:25
Решение 1
1) сначала заметим, что есть прямой рейс из аэропорта ОКТЯБРЬ в СОСНОВО с прибытием в 17:25:
2) посмотрим, сможет ли путешественник оказаться в СОСНОВО раньше этого времени, если полетит через другой аэропорт, с пересадкой
3) можно лететь, через КРАСНЫЙ, но, как следует из расписания,
путешественник не успеет на рейс КРАСНЫЙ – СОСНОВО, который улетает в 13:15, то есть на 15 минут раньше, чем в КРАСНЫЙ прилетает самолет ОКТЯБРЬ – КРАСНЫЙ
4) можно лететь через БЕРЕГ,
но рейс БЕРЕГ – СОСНОВО вылетает даже раньше, чем рейс ОКТЯБРЬ – БЕРЕГ, то есть, пересадка не получится
5) поскольку даже перелеты с одной пересадкой не стыкуются по времени, проверять варианты с двумя пересадками в данной задаче бессмысленно (хотя в других задачах они теоретически могут дать правильное решение)
6) таким образом, правильный ответ – 4 (прямой рейс).
- можно не заметить, что путешественник не успеет на пересадку в КРАСНОМ (неверный ответ 15:40)
- можно перепутать аэропорты вылета и прилета (неверный ответ 16:35)
Решение 2
1) для решения можно построить граф, показывающий, куда может попасть путешественник из аэропорта ОКТЯБРЬ
2) из аэропорта ОКТЯБРЬ есть три рейса:
3) построим граф, около каждого пункта запишем время прибытия
4) проверим, не будет ли быстрее лететь с пересадкой: рейс «КРАСНЫЙ-СОСНОВО» вылетает в 13:15, то есть, путешественник на него не успевает; он не успеет также и на рейс «БЕРЕГ-СОСНОВО», вылетающий в 12:15
5) таким образом, правильный ответ – 4 (прямой рейс).
Дороги
Грунтовая дорога проходит последовательно через населенные пункты А, B, С и D. При этом длина дороги между А и В равна 80 км, между В и С – 50 км, и между С и D – 10 км. Между А и С построили новое асфальтовое шоссе длиной 40 км. Оцените минимально возможное время движения велосипедиста из пункта А в пункт В, если его скорость по грунтовой дороге – 20 км/час, по шоссе – 40 км/час.
1) 1 час 2) 1,5 часа 3) 3,5 часа 4) 4 часа
Решение
1) нарисуем схему дорог, обозначив данные в виде дроби (расстояние в числителе, скорость движения по дороге – в знаменателе):
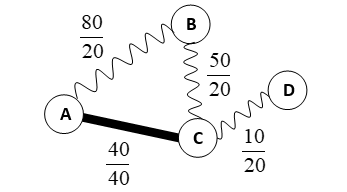
2) разделив числитель на знаменатель, получим время движения по каждой дороге
3) ехать из А в B можно
- напрямую, это займет 4 часа, или ...
- через пункт C, это займет 1 час по шоссе (из А в С) и 2,5 часа по грунтовой дороге (из В в С), всего 1 + 2,5 = 3,5 часа
4) таким образом, правильный ответ – 3.
- можно не заметить, что требуется найти минимальное время поездки именно в В, а не в С (неверный ответ 1 час)
- можно ограничиться рассмотрением только прямого пути из А в В и таким образом получить неверный ответ 4 часа
- можно неправильно нарисовать схему
Стоимость перевозок
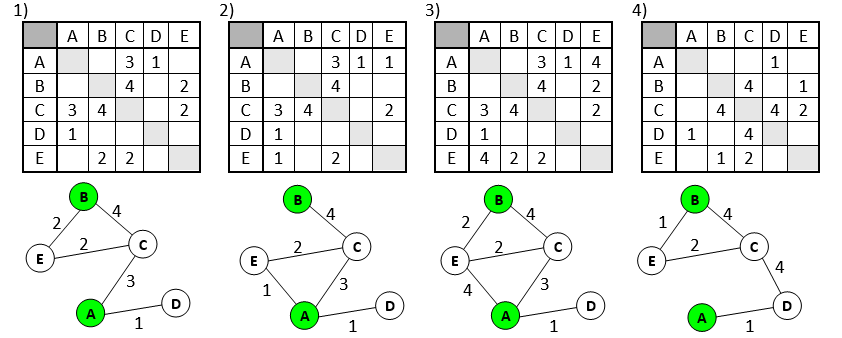
Р-01. Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними. Укажите таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в B не больше 6». Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями.
Решение
1) нужно рассматривать все маршруты из А в В, как напрямую, так и через другие станции 2) рассмотрим таблицу 1:
- из верхней строки таблицы следует, что из А в В напрямую везти нельзя, только через C (стоимость перевозки А-С равна 3) или через D (стоимость перевозки из А в D равна 1)
- предположим, что мы повезли через C; тогда из третьей строки видим, что из C можно ехать в В, и стоимость равна 4
- таким образом общая стоимость перевозки из А через С в В равна 3 + 4 = 7
- кроме того, из С можно ехать не сразу в В, а сначала в Е:
а затем из Е – в В (стоимость также 2),
так что общая стоимость этого маршрута равна 3 + 2 + 2 = 7
- теперь предположим, что мы поехали из А в D (стоимость 1); из четвертой строки табли-цы видим, что из D можно ехать только обратно в А, поэтому этим путем в В никак не по-пасть:
- таким образом, для первой таблицы минимальная стоимость перевозки между А и В равна 7; заданное условие «не больше 6» не выполняется
3) аналогично рассмотрим вторую схему; возможные маршруты из А в В:
4) для третьей таблицы:
5) для четвертой:
6) условие «не больше 6» выполняется только для таблицы 3
7) таким образом, правильный ответ – 3.
- метод ненагляден, легко запутаться и пропустить решение с минимальной стоимостью
Решение 2
1) для каждой таблицы нарисуем соответствующую ей схему дорог, обозначив стоимость перевозки рядом с линиями, соединяющими соседние станции:
2) теперь по схемам определяем кратчайшие маршруты для каждой таблицы:
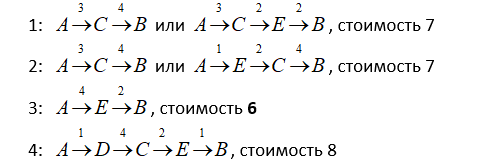
3) условие «не больше 6» выполняется только для таблицы 3
4) таким образом, правильный ответ – 3.
- нужно внимательно строить схемы по таблицам, этот дополнительный переход (от таб-личных моделей к графическим) повышает наглядность, но добавляет еще одну возмож-ность для ошибки
- наглядность схемы зависит от того, как удачно вы выберете расположение ее узлов; один из подходов – сначала расставить все узлы равномерно на окружности, нарисовать все связи и посмотреть, как можно расположить узлы более удобно
- по невнимательности можно пропустить решение с минимальной стоимостью