Теория

Единицы измерения

Любая информация, хранящаяся на компьютере, представлена в двоичном коде. Её размер определяется кол-вом занятых бит. Бит - это наименьшая величина хранения информации, может принимать одно из двух значений: 0 или 1.

Биты объединяются в байты, в одном байте помещается 8 бит

$$1 \text{байт}=2^3 \text{бит}$$

В отличие от физических величин, все производные од байта отличаются между собой не в $10^3$ раз, как килограмм и грамм, а в $2^{10}$ раз.

Поэтому

$$1 \text{Кбайт}= 2^{10}\text{байт} = 2^{13}\text{бит}$$

$$1 \text{Мбайт} = 2^{10}\text{Кбайт}=2^{20}\text{байт}=2^{23}\text{бит}$$

При передаче информации можно измерить её скорость $v$. Она равна частному между объёмом переданной информации $o$ и временем её передачи $t$

$$v = \frac{n}{t}$$

Если количество информации измерялось в битах, то скорость будет измерять в бит/с.

Большие числа. Что делать?

Обычно (хотя и не всегда) задачи, в условии которых даны большие числа, решаются достаточно просто, если выделить в этих числах степени двойки. На эту мысль должны сразу наталкивать такие числа как

$$128 = 2^7, ~ 256 = 2^8, ~ 512 = 2^9 ,~ 1024 = 2^{10},$$

$$2048 = 2^{11}, ~4096 = 2^{12}, ~8192 = 2^{13},~ 16384 = 2^{14},~ 65536 = 2^{16}$$

Нужно помнить, что соотношение между единицами измерения количества информации также представляют собой степени двойки:

$1$ байт = $8$ бит = $23$ бит,

$1$ Кбайт = $1024$ байта = $2^{10}$ байта = $2^{10} * 2^{3}$ бит = $2^{13}$ бит

$1$ Мбайт = $1024$ Кбайта = $2^{10}$ Кбайта = $2^{10} * 2^{10}$ байта = $2^{20}$ байта= $2^{20} * 2^{3}$ бит = $2^{23}$ бит

при умножении степени при одинаковых основаниях складываются

$$2^a*2^b=2^{a+b}$$

а при делении – вычитаются:

$$2^a/2^b=2^{a-b}$$

Кодирование информации

При кодировании данных, т.е. переводе из понятных человеку данных в биты используется два рода кодирования: первый - это равномерный двоичный, второй - неравномерный.

Равномерный код

В программировании для хранения переменных используется так называемый равномерный двоичный код. Под каждую переменную массива выделяется одинаковое количество бит, кратное 8. Иначе говоря, под каждую переменную выделяется целое количество байт.

расстояния Хэмминга

Для двух равномерных кодов можно определить количество позиций, в которых одно кодовое слово отличается от другого. Эту величину называют расстояние Хэмминга.

Например, коды 101 и 111 имеют расстояние Хэмминга, равное одному, коды 1100 и 0110 - равное двум.

Неравномерный код

Если набор значений заранее предопределён, то каждому из них можно сопоставить свой уникальный двоичный код (последовательность бит), причём коды у значений могут иметь разную длину.

Тогда, читая биты последовательно, можно восстановить, какому значению соответствует та или иная последовательность. При этом наиболее часто встречаемым значениям мы можем связать с "короткими" последовательностями, а редко встречаемые - с "длинными". Это позволит нам ещё больше сэкономить память. На этом принципе построены многие архиваторы.

условие Фано

Правда, для однозначной интерпретации кодов, необходимо, чтобы каждый код не является такой последовательностью битов, с которой начинается какой-либо другой код. Это условие называется прямым условием Фано.

Это требование неслучайно. Если один код является началом другого, то в момент его чтения возникает неоднозначное поведение. Ведь мы читаем биты последовательно. После прочтения очередного бита программе будет неясно, что делать: толи нужно решить, что этот код закончился и надо читать следующий, толи нужно дочитать код до конца.

В задачах егэ условие Фано иногда трактуется так: все коды находятся в листьях дерева, т.е. в вершинах, из которых не выходит ни одного ребра

Например, если у нас есть четыре буквы A, B, C, D и при этом коды первых трёх мы определили так:

A	B	C
10	11	001

то код буквы D не может быть 00, потому что 00 уже содержится в коде C, 11 - недопустимо, потому что содержится в коде B

Однако, если мы поменяем все коды на трёхзначные

A	B	C
100	110	010

Тогда для D будет доступен код 00.

Подбирать вручную коды для разных элементов - довольно трудоёмкая задача. Для этого существует готовый алгоритм. Он называется Алгоритм Хаффмана.

Правда в оригинальном алгоритме символы строки сначала сортируются, а потом на их основе строится дерево декодирования. В задачах ЕГЭ даётся просто последовательность букв, и на её основе требуется построить дерево декодирования и что-то о нём сказать.

В блоке теории рассмотрим алгоритм Хаффмана полностью, а в примерах, будем использовать только ту часть, которая работает уже с отсортированными по частоте встречаемости буквами. Сам алгоритм способен работать с любыми данными, однако в случае строки - получается наиболее наглядно.

Допустим, мы хотим закодировать строку "Carpe diem, memento mori!". Если на каждый символ мы выделим по 1 байту, то вся строка при использовании равномерного двоичного кода занимала бы 25 байт или 25*8=200 бит, т.к. её длина равна 25.

Для начала посчитаем частоты всех символов:

C	a	r	p	e		d	i	m	,	n	t	o	!
1	1	2	1	4	3	1	2	4	1	1	1	2	1

Напомню, дерево декодирования - это в первую очередь дерево, т.е. граф, не имеющий циклов. Помимо этого, у дерева декодирования из каждой вершины может выходить не больше двух рёбер.

Чтобы построить такое дерево, составим новую таблицу, упорядочив встречаемость по возрастанию. Дальше встречаемость будем называть просто весом.

Символом

обозначается пробел.

Общая идея построения дерева такая: мы берём две вершины с самым малым весом, выкидываем их из списка и добавляем новый элемент, имеющий вес, равный сумме двух выкинутых в список так, чтобы он оставался упорядоченным.

На первом шаге необходимо выкинуть символы C и A.

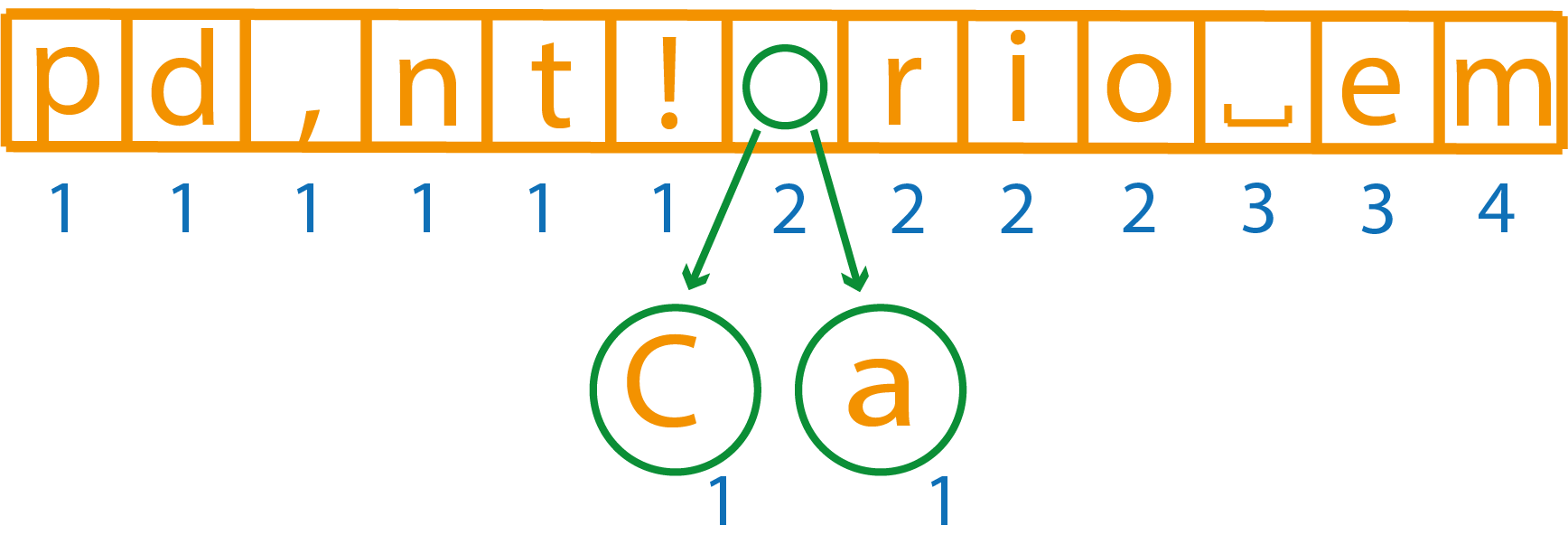
Таким же образом соединим оставшиеся вершины с весом 1.

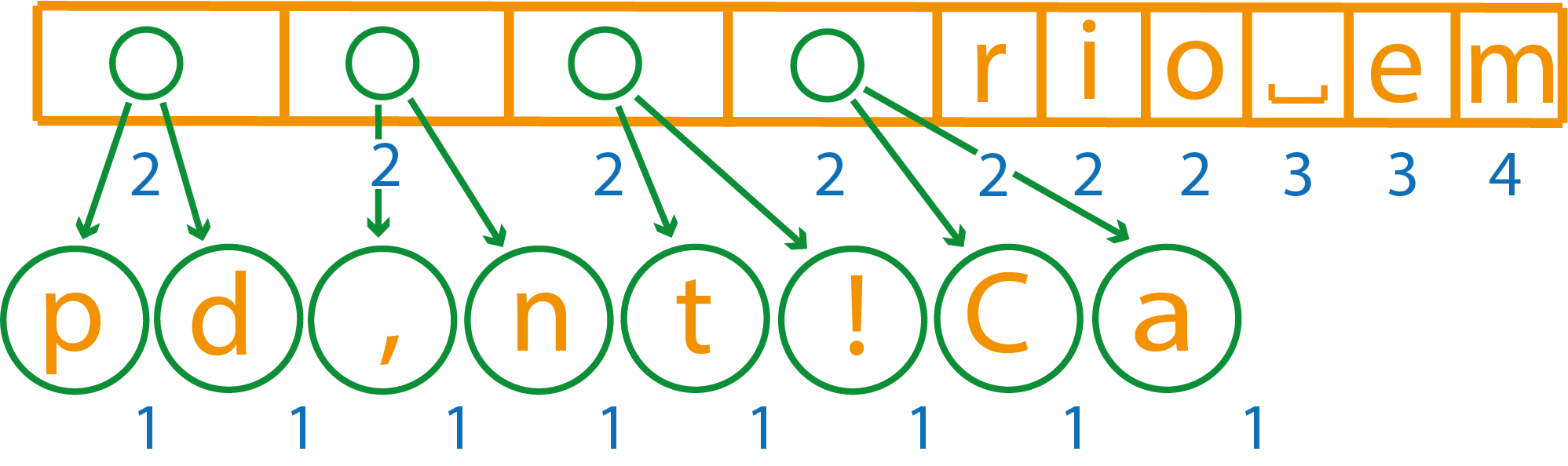
Теперь объединим первые два элемента с весом 2

Снова объединим первые два элемента весом 2

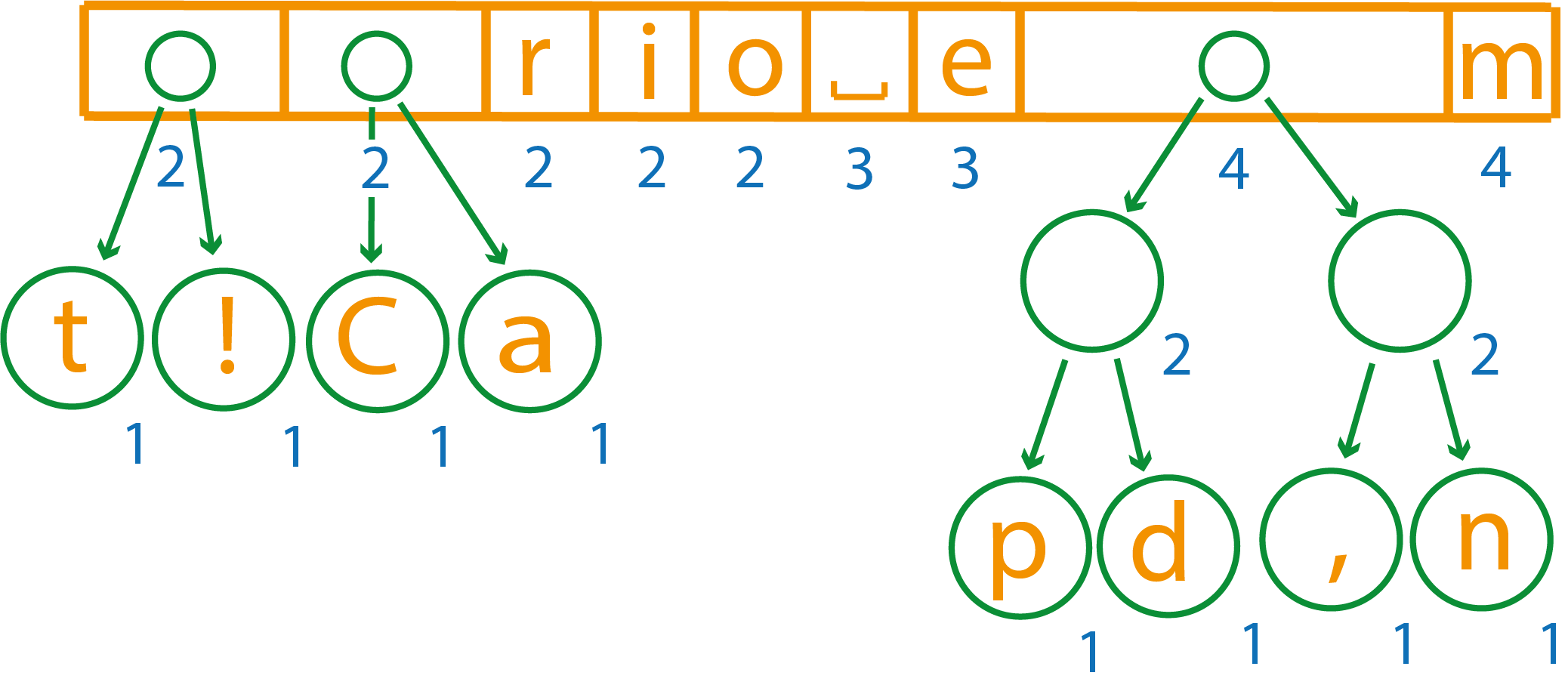
И объединим оставшиеся

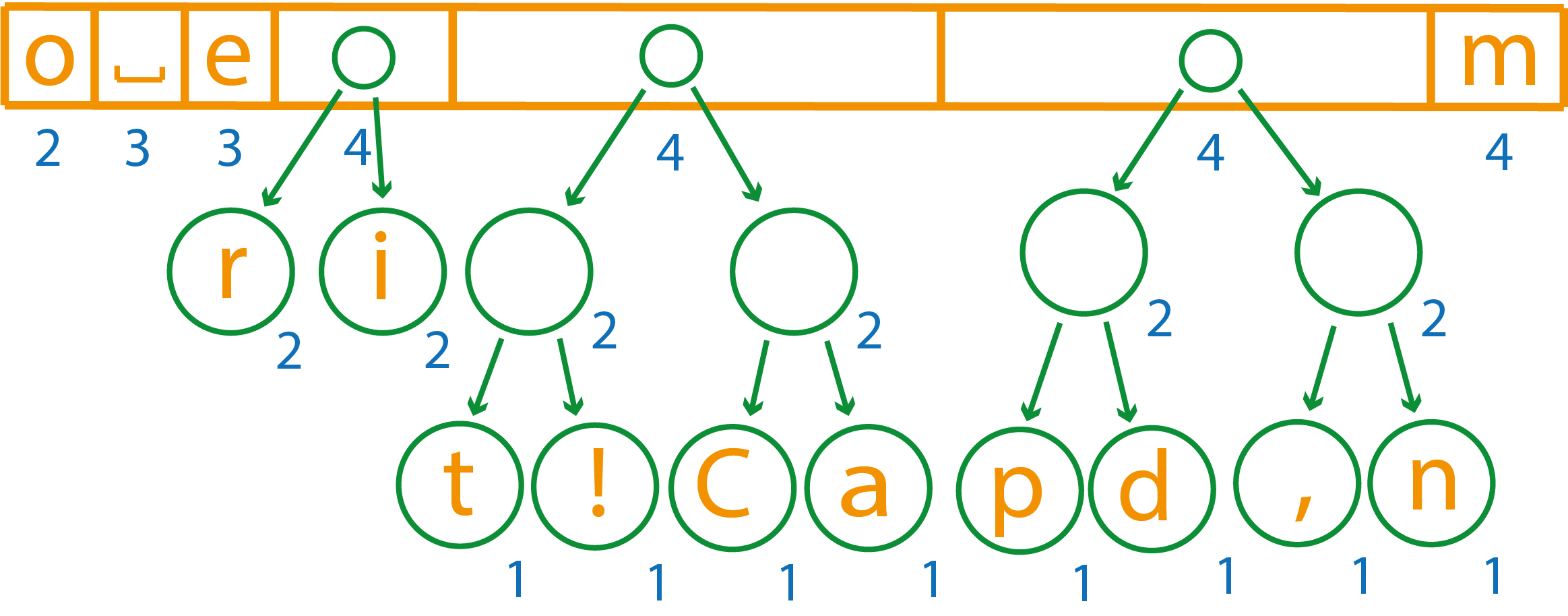
Теперь первые два элемента имеют вес 2 и 3, объединим их в элемент весом пять и поставим в самый конец, т.к. веса остальных элементов меньше

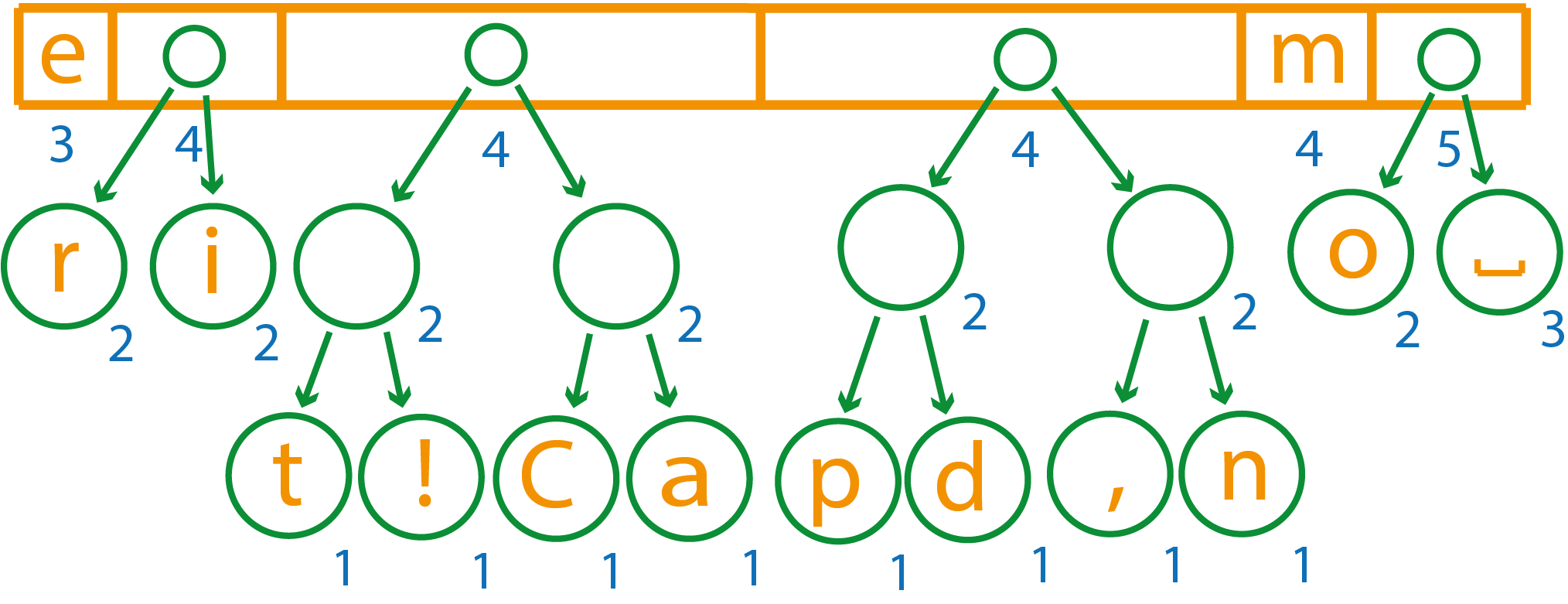
Снова объединим первые два элемента

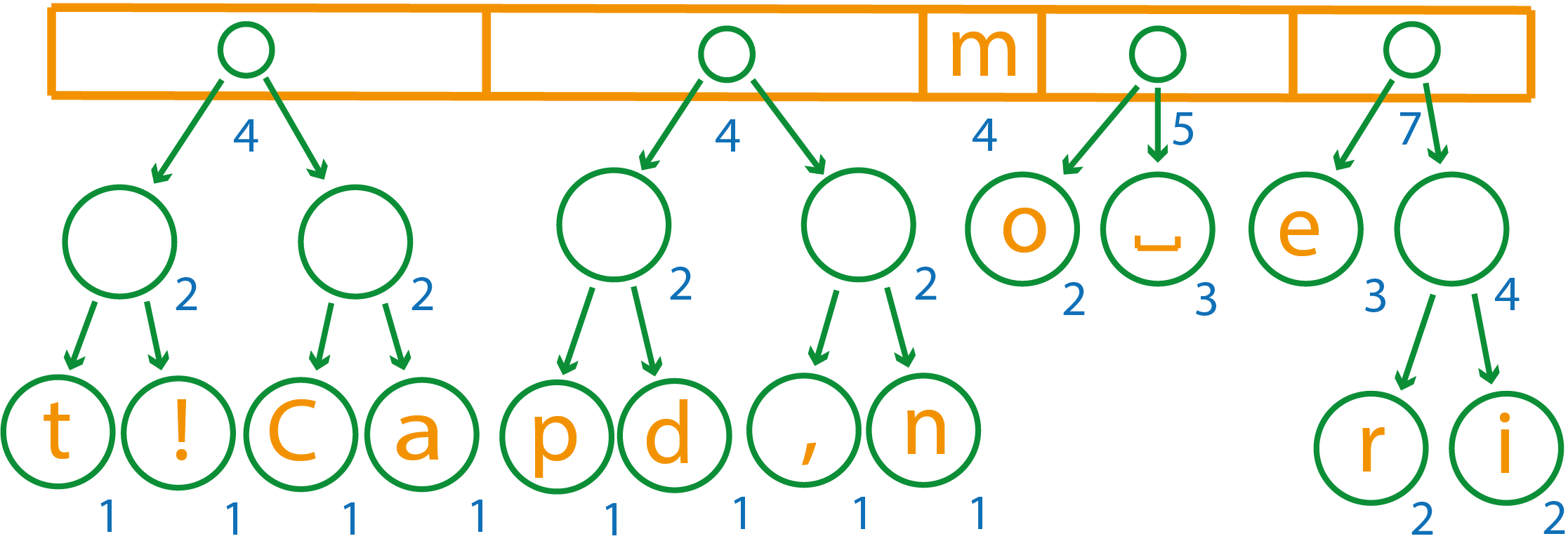
Первые два элемента имеют вес 4 и 5, при объединении они дадут вес 9, поэтому полученный новый элемент нужно будет перенести в конец списка

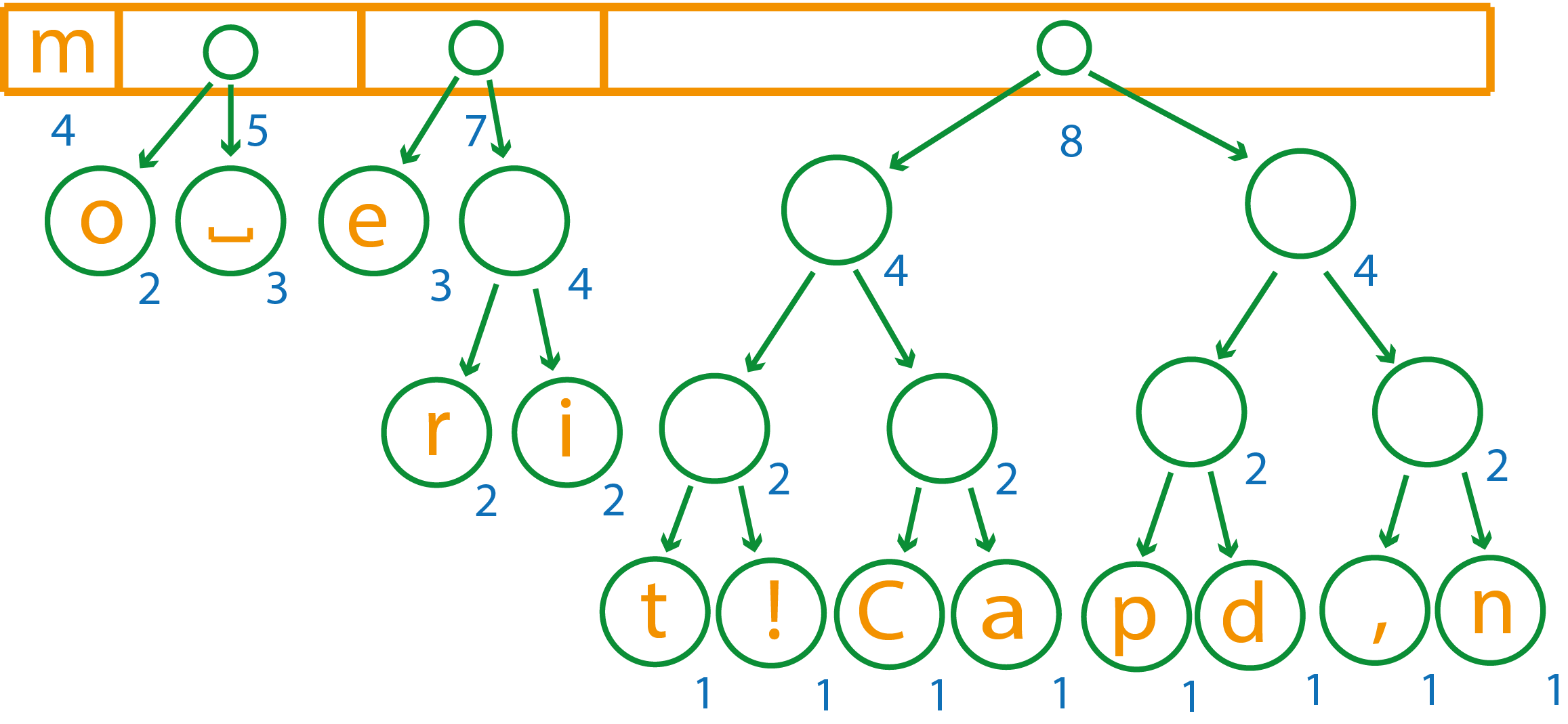
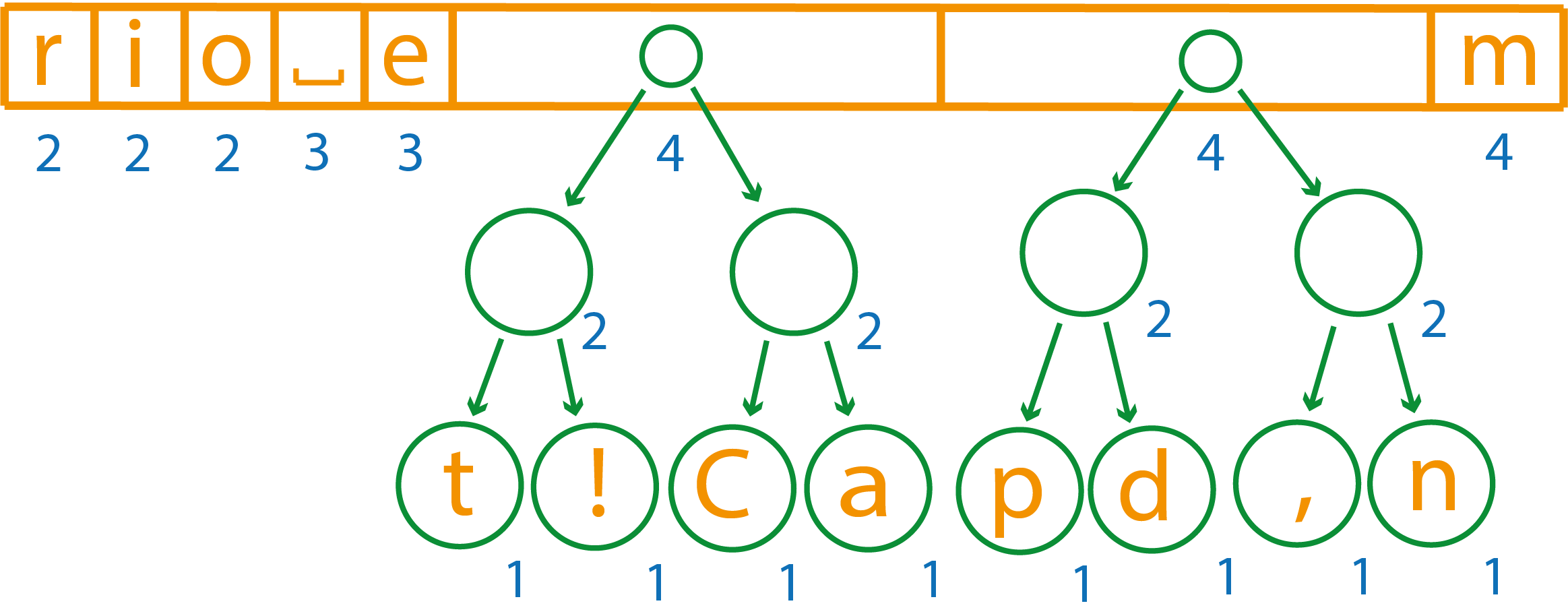
В списке элементов осталось всего три, объединяем два первых элемента, т.к. у третьего вес больше в силу отсортированности списка

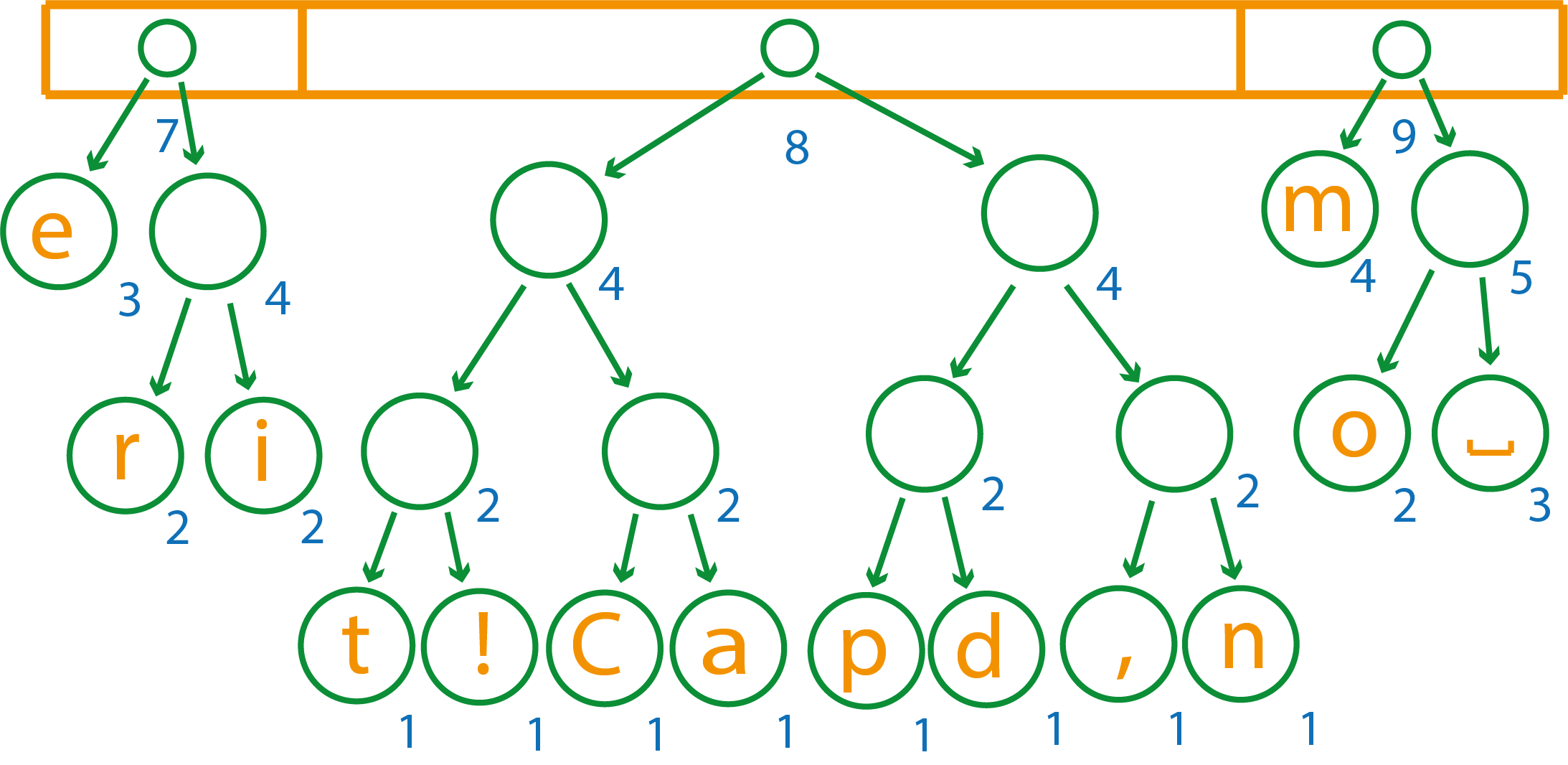
После объединения осталось два элемента, их останется только собрать в единое дерево

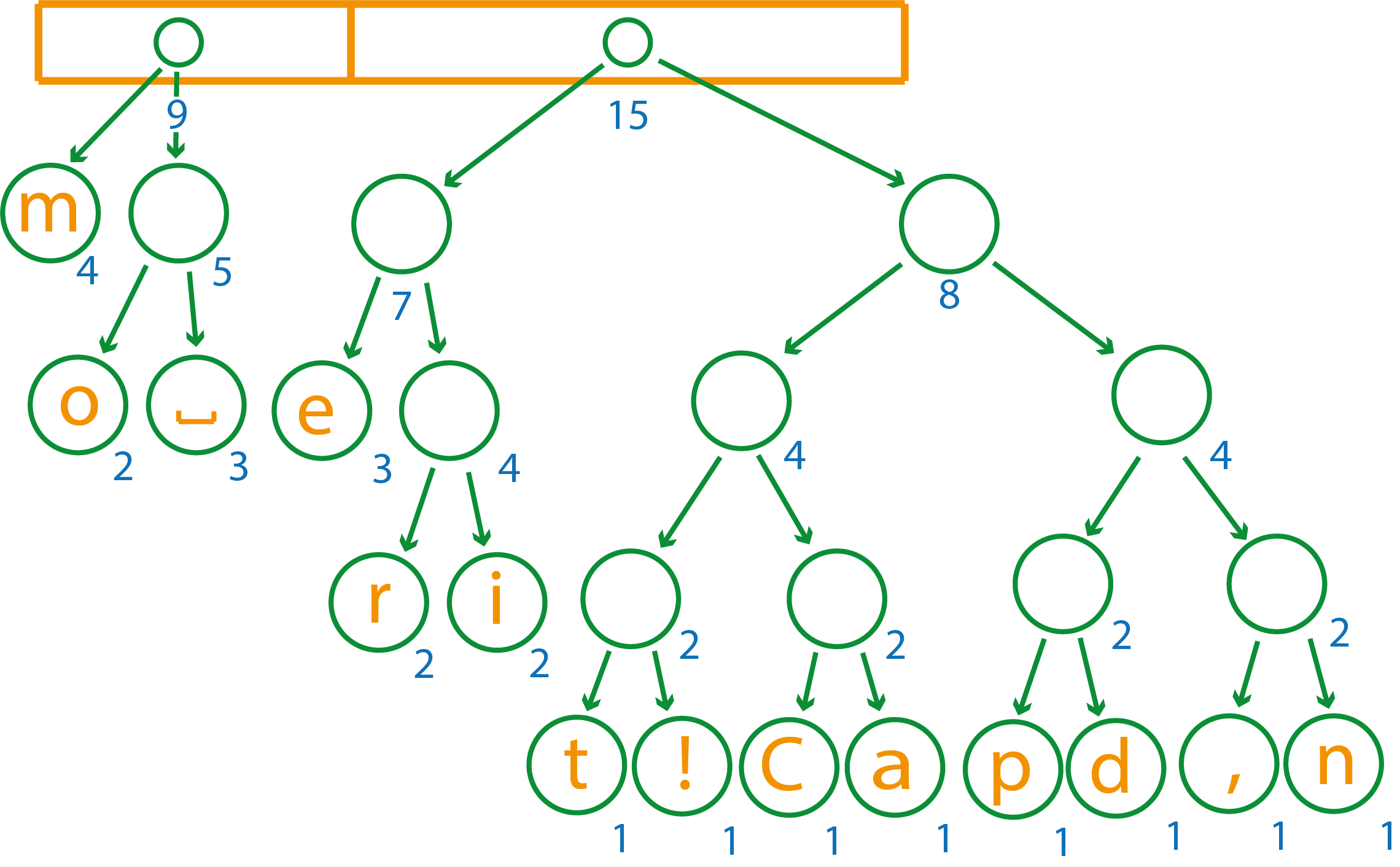
Итоговое дерево будет выглядеть так

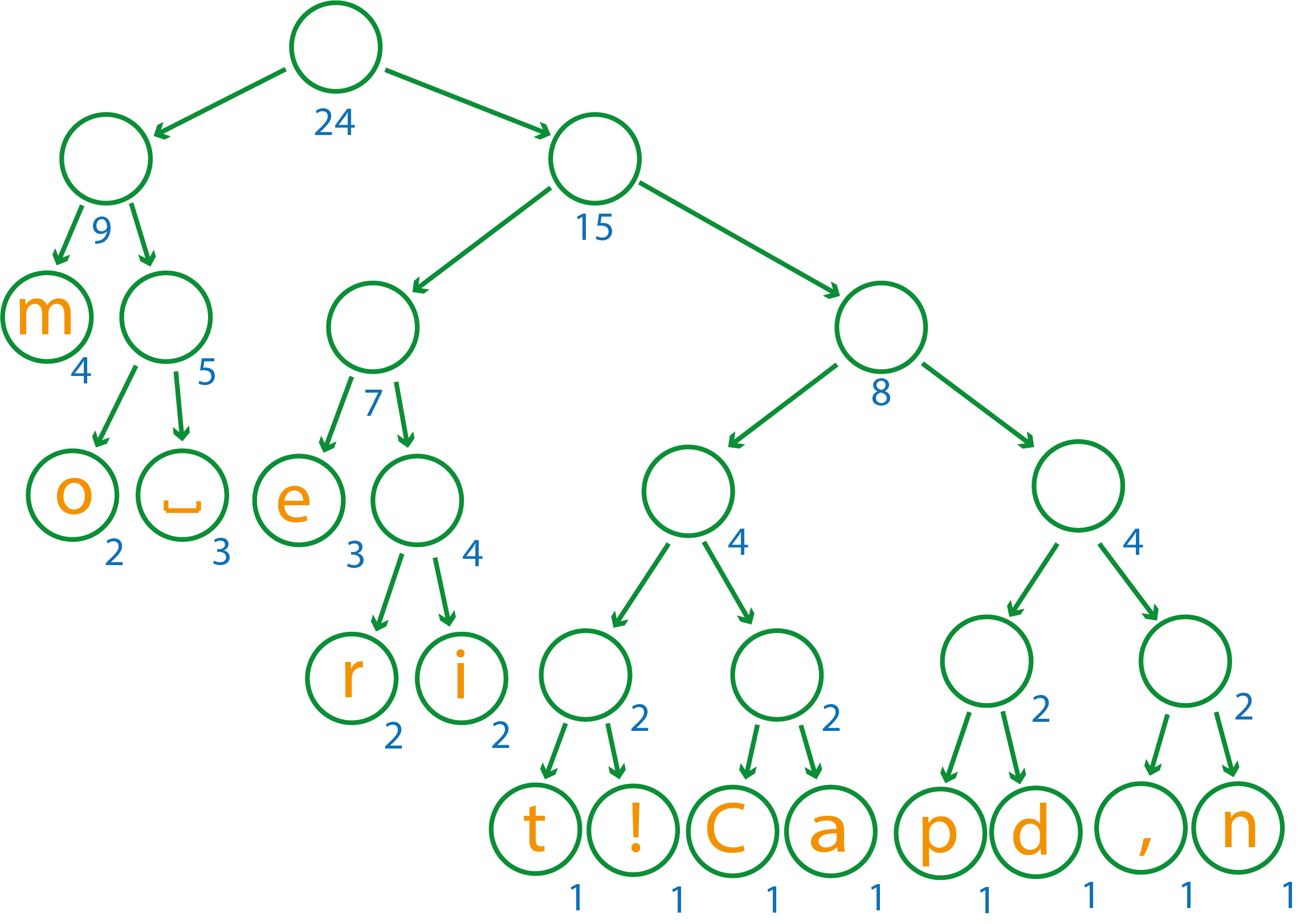
Чтобы оно стало деревом декодирования, необходимо на каждом ветвлении расставить по 0 и 1

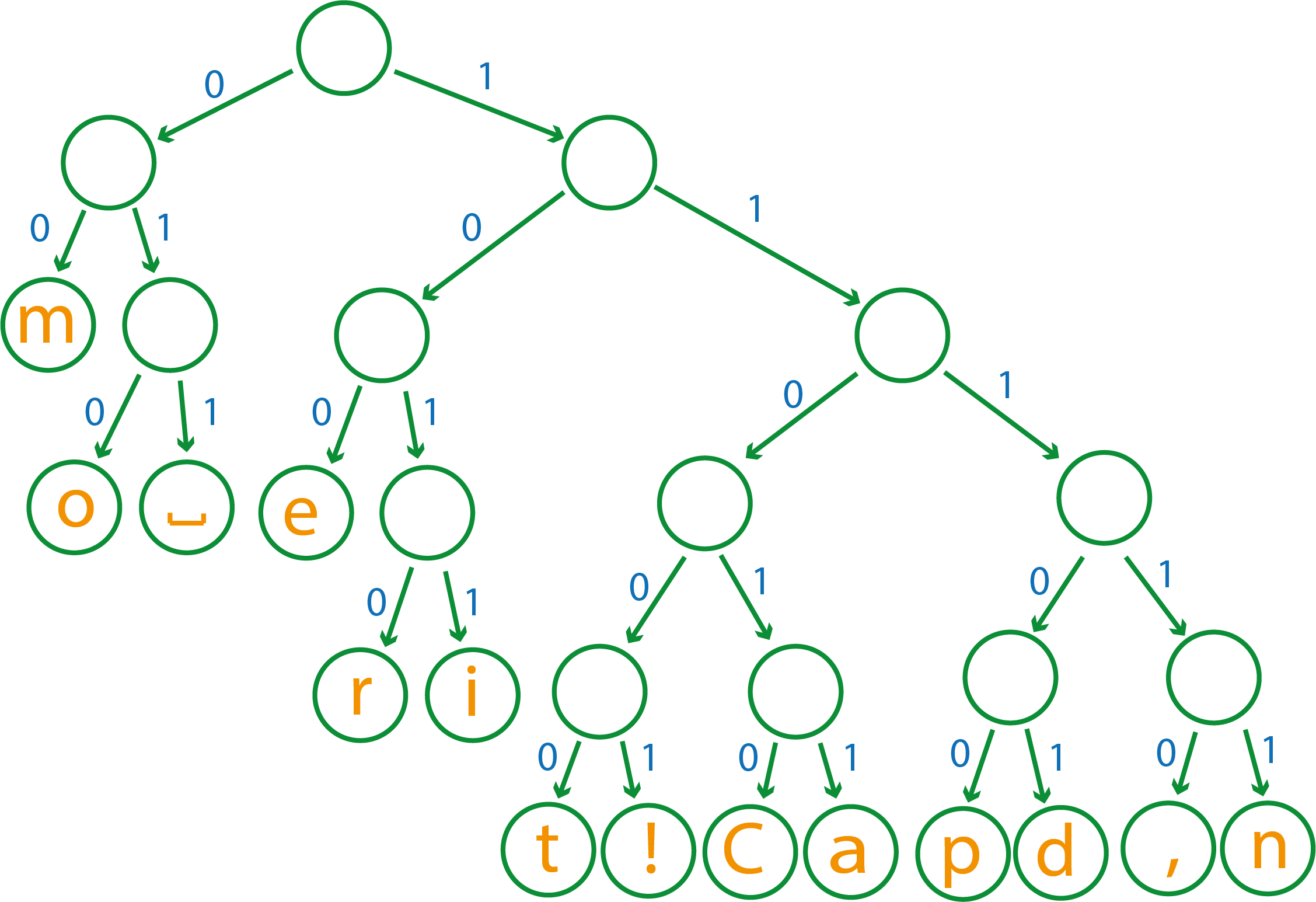
Теперь, чтобы получить код того или иного символа, нужно просто пройти от единого корня дерева (самая верхняя вершина) до нужной нам. При переходе от одной вершины к другой необходимо добавлять в код то число, которое написано на соответствующем ребре.

Например, буква e будет иметь код 100

Таким же образом определим остальные коды:

C	a	r	p	e		d	i	m	,	n	t	o	!
11010	11011	1010	11100	100	011	11101	1011	00	01	11111	11001	010	1011