5. Вещественные числа

Теория

Хранение вещественных чисел в оперативной памяти - далеко не такая простая задача, как хранение целых.

Можно придумать много разных способов хранения вещественных чисел, но все они сводятся к одному и тому же ограничению. Любое вещественное число мы можем хранить до определённой степени точности.

Строго говоря, вещественными числами в программировании называются рациональные.

В любом случае нам придётся хранить сами цифры числа, а также место, куда следует поставить точку.

Если все биты будут заполнены цифрами, то мы сможем довольно точно задать число, однако такой подход даёт очень узкий диапазон значений. Для большей универсальности используют вещественные числа, представленные в экспоненциальной форме:

$$X = S\times M\times N^q,$$

где $X$ – вещественное число, $S$ - знак числа, $M$ - мантисса числа, $N$ - основание системы счисления, а $q$ - степень, часто называется порядком.

Например, в числе $6.6261\times 10^{-27}$ мантисса $M=6.6261$, основание $N=10$, степень $q=-27$, знак $S=1$.

По общему соглашению $0.1 \le M\lt 10$. Это позволяет не определять, где стоит точка в мантиссе. Она всегда будет после первой цифры.

Процессоры работают только с числами, у которых $N$ равно $2$.

В java есть два типа данных: float и double. Первый - это вещественные данные одинарной точности, второй - двойной. Обычно используется double.

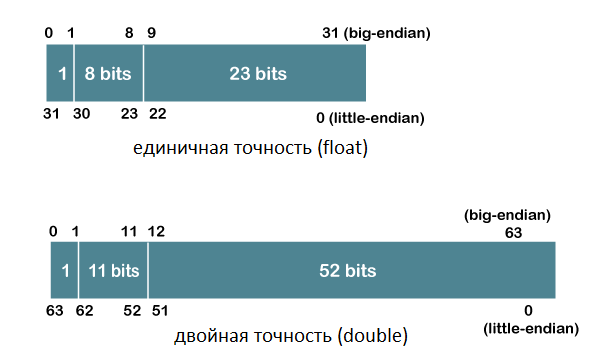
Первый бит всегда задаёт знак числа.

Биты	float	double
Знак	1	1
Степень(Экспонента)	8	11
Мантисса	23	52

Подробная информация по типам данных java представлена в следующей таблице:

Тип	Размер	Значение по умолчанию	Точность	Значащие цифры	Диапазон
float	32 бита (4 байта)	0.0f	Единичная	6	от 3.4e-038 до 3.4e+038
double	64 бита (8 байт)	0.0d	Двойная	15	от 1.7e-308 до 1.7e+308

Операции над вещественными числами, представленными в экспоненциальной форме довольно муторные в плане реализации на логических элементах, о них можно прочитать здесь и здесь

Чтобы вывести вещественное число на экран, можно воспользоваться уже известной нам командой print(), например:

double d = 1.0 / 3;
System.out.print(d);

Получим:

0.3333333333333333

Такой вывод получается довольно громоздким. В java есть готовый инструмент для настраиваемого вывода числа. Этот инструмент называется форматирование.

Форматирование работает так: сначала указывается строка, в которой особым способом указывается, как именно должно быть отображено число, а потом само число, которое нужно отобразить.

Например, чтобы вывести число с точностью до трёх знаков после запятой, нужно выполнить команду

double d = 1.0 / 3;
System.out.printf("%.3f",d);

Получим:

0,333

Обратите внимание: мы использовали новую команду printf(), а не print(). Последняя буква f означает форматирование. Также у выведенного вместо точки ввыодится запятая.

Это происходит из-за того, что обозначение символа разделения зависит от языка. Если у компьютера задан русский язык системы, то символом разделения будет запятая ,, если английский - то ..

важно

У ситемы тестирования задан английский язык, поэтому в примерах будут даны числа через ., а вводить их на компьютере нужно используя ,.

Какое число стоит после точки в первом аргменте, столько символов после запятой будет выведено. Например, следующая команда выведет вещественное число d с точностью до одного знака после запятой.

double d = 1.0 / 3;
System.out.printf("%.1f",d);

получим:

0,3

В строку можно подставлять любое количество чисел, правда, нужно для каждого из них указать, куда именно вставлять его с помощью последовательности символов %.f. Для каждого числа количество цифр указывается отдельно.

double a = 1.0 / 9;
double b = 2.0 / 9;
double c = 4.0 / 9;
System.out.printf("%.4f %.3f %.2f", a, b, c);

Получим:

0,1111 0,222 0,44

Обратите внимание: для ввода вещественных костант необходимо использовать литерал вида: 1.0. Если не добавить .0, то java будет считать число целым, и будет выполнено целочисленное деление

double a = 1.0 / 9;
double b = 1 / 9;
System.out.printf("%.3f %.3f", a, b);

Получим:

0,111 0,000

Чтобы прочитать вещественное число, нужно использовать соответствующие команды сканера:

Scanner scanner = new Scanner(System.in);
double a = scanner.nextDouble();
float f = scanner.nextFloat();

Хотя вещественных типов данных два, мы будем работать только с double.

Чтобы преобразовать вещественное число в целое, т.е. взять целую часть, нужно использовать явное приведение типов. Чтобы сделать явное преобразование типов, нужно добавить в скобочках (тип) перед переменной:

   double a = 12.231;
   int b = (int)a;
   System.out.println(b);

Получим:

12

Для перевода целых чисел в вещественные не нужно явного преобразования, java выполняет такие преобразования автоматически, поэтому они называются неявными.

   int a = 100;
   double b = a;
   System.out.printf("%.3f", b);

Получим:

100,000

Однако если у нас есть целое число, а мы хотим разделить его как вещественное, нужно использовать явное приведение типов:

int a = 10;
double r = (double) a / 3;
System.out.println(a / 10);
System.out.printf("%.3f", r / 10);

Получим:

1
0,333

Так происходи тиз-за того, что java решает, какое деление нужно выполнить: целочисленное или вещественное по типам данных переменных. Если хотя бы одна переменная вещественная, то деление будет вещественным.

Математические действия

// вещественные операции Math
answ = Math.sqrt(a); // корень
answ = Math.tan(a);  // тангенс
answ = Math.atan2(y,x); // арктангенс
answ = Math.sin(a);  // синус
answ = Math.cos(a);  // косинус
answ = Math.round(b);    // округление
answ = Math.log(b);    // логарифм
answ = Math.PI;  // число Пи
answ = Math.pow(a,b);  // возведение числа a в степень b

// операции, работающие и с целыми, и с вещественными числами

// целые числа
int a = 10;
int b = 15;

int c = Math.abs(a); // модуль
int d = Math.max(a, b); // большее из двух чисел
int e = Math.min(a, b); // меньшее из дух чисел

// вещественные числа
double af = 10.0;
double bf = 10.0;

double cf = Math.abs(af); // модуль
double df = Math.max(af, bf); // большее из двух чисел
double ef = Math.min(af, bf); // меньшее из дух чисел

Функция atan2() принимает в качестве аргументов координаты точки $x$ и $y$, это позволяет получить угол наклона в диапазоне $[-\pi,~\pi)$, если использовать классическую функцию арктангенса atan(), то она принимает в качестве аргумента одно число, равное отношению $y$ координаты точки к $x$ координате.

Из-за этого обычный арктангенс atan() позволяет получить угол в диапазоне $[-\frac{\pi}{2},~\frac{\pi}{2})$.

Формулы

Среднее арифметическое двух чисел $a$ и $b$ вычисляется по формуле:

$$S = \frac{a+b}{2}$$

Среднее геометрическое - по формуле:

$$V = \sqrt{a*b}$$

Задание

1. Известно, что $x$ кг конфет стоит $n$ рублей. Определить, сколько стоит $1$ кг и $m$ кг этих же конфет. Ответ выведите с точностью до трёх знаков после запятой.
2. Даны два числа $a$ и $b$. Найти их среднее арифметическое. Ответ выведите с точностью до двух знаков после запятой.
3. Известно, что $X$ кг шоколадных конфет стоит $A$ рублей, а $Y$ кг ирисок стоит $B$ рублей. Определить, сколько стоит $1$ кг шоколадных конфет, $1$ кг ирисок, а также во сколько раз шоколадные конфеты дороже ирисок. Ответ выведите с точностью до трёх знаков после запятой.
4. Даны два неотрицательных числа $a$ и $b$. Найти их среднее геометрическое.
5. Даны два ненулевых числа. Найти сумму, разность, произведение и частное их квадратов.
6. Даны два ненулевых числа. Найти сумму, разность, произведение и частное их модулей.
7. У Васи в квартире установлен двухтарифный электрический счетчик. Он измеряет потребление электроэнергии в дневное время по тарифу $Т_1$ и в ночное время по тарифу $Т_2$. Вася снял показания счетчика: в начале месяца по каждому тарифу ($Т_{1_н}$ и $Т_{2_н}$) и в конце месяца ($Т_{1_к}$ и $Т_{2_к}$). Вася знает, что стоимость киловатт-часа электроэнергии составляет по дневному тарифу $c_1$, а по ночному тарифу $c_2$. На вход программе подается: в первой строке: $Т_{1_н}$ (в кВт·ч), во второй строке: $Т_{2_н}$ (в кВт·ч), в третьей строке: $Т_{1_к}$ (в кВт·ч), в четвертой строке: $Т_{2_к}$ (в кВт·ч), в пятой строке: $c_1$ (в рублях), в шестой строке: $c_2$ (в рублях). Ваша программа должна вывести на экран: в первой строке: количество потребленной электроэнергии по каждому тарифу (в кВт·ч), во второй строке: сумму, которую нужно заплатить по каждому тарифу (в рублях), в третьей строке - общую сумму счета за электроэнергию (в рублях). Числа в строках выводить через пробел, с точностью $2$ знака после десятичной точки.

Ссылка на контест