Вычислители

Процессор может не только хранить числа в своих регистрах, но и производить операции над ними.

Сумматор

Мы начали рассмотрение принципов работы центрального процессора с суммирования. Это - самая простая арифметическая операция с точки зрения её реализации на логических элементах.

Полусумматор

Попробуем построить систему, состоящую из примитивных логических элементов, которая умеет складывать два бита следующим образом. У системы есть два входа, каждый из них может принимать значение 0 и 1.

Выхода нам понадобится тоже два. Первый будет отвечать за переполнение, а второй за сумму. Т.к. у нас всего два значения в множестве логических значений, то при сложении $1+1$ мы по идее должны выйти за границы множества. Чтобы разрешить такую ситуацию, как раз и вводят двоичную многоразрядную систему счисления.

При переполнении мы должны увеличивать на 1 следующий бит. Нумерация разрядов-битов идёт справа налево. Младший бит имеет номер 0. Степени двойки, на которое домножаются значения разрядов, соответствуют их порядковым номерам.

Если мы складываем $1001_2$ и $101_2$, то нулевой, т.е. младший разряд переполнится, мы это запомним, а младший разряд суммы обнулим, добавим его к следующему разряду и сложим следующие разряды. В нашем случае первый разряд суммы равен 1, потому что оба первых разряда слагаемых равны 0, но мы перенесли дополнительную единицу от сложения предыдущих разрядов. Пройдя так до конца, получим число $1110_2$.

Чтобы построить такой вычислитель, нам нужно сначала построить полусумматор. Т.е. такое устройство, которое будет складывать два бита, но не будет учитывать перенос от предыдущих.

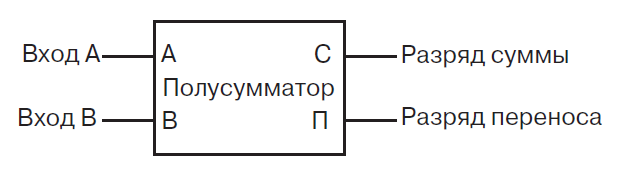
Именно из-за неполного функционала полусумматор так и называется. Построить его несложно.

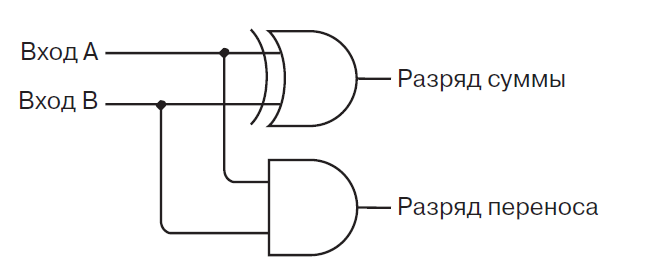
Разряд переноса будет единицей тогда и только тогда, когда оба входа равны единице. Иначе разряд не переполнится. С разрядом суммы немного сложнее. Для этого нам понадобится операция xor (ксор). Разряд суммы должен быть равен $1$ только когда ровно один из аргументов равен $1$. На базовых элементах логики реализовать xor несложно. Вот его схема:

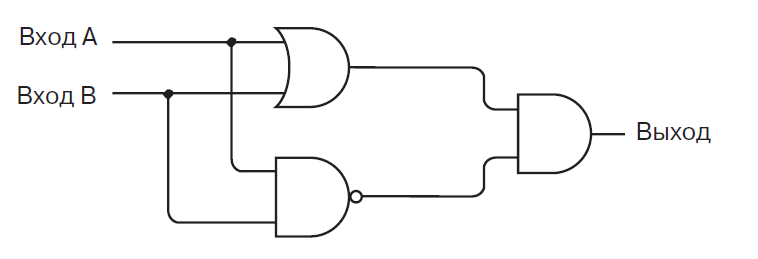
Верхний левый блок - это логическое ИЛИ, остальные два - это логическое И. Правда, выход одного инвертирован: $0$ становится $1$, $1$ становится $0$. Инвертирование обозначается кружком.

Если обозначить за $p$ - разряд переноса, а за $s$ - сумму, то получим выражения:

$$p = (a\land b),\\ p = (a\land b), s = (a\lor b)\land\lnot p,$$

где - $\land$ - логический оператор И, а $\lor$ - логический оператор ИЛИ

Если немного преобразовать выражение для $s$, получим:

$$s = (a\lor b)\land\lnot(a\land b)=(a\lor b)\land(\lnot a\lor\lnot b)$$

Иными словами, сумма равна $1$ тогда и только тогда, когда слагаемые биты различны. Это и есть наш xor. В математике он обозначается $\oplus$.

Это преобразование мы выполнили используя тождество $\lnot(a\land b)=\lnot a \lor\lnot b$

Подробнее о тождествах рассказано в соответствующем разделе.

Сам xor обозначается так

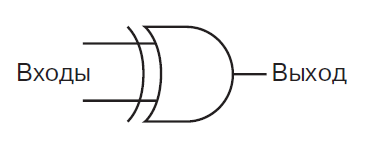
Тогда полусумматор можно построить по следующей схеме:

Сложение

Соединим последовательно два полусумматора

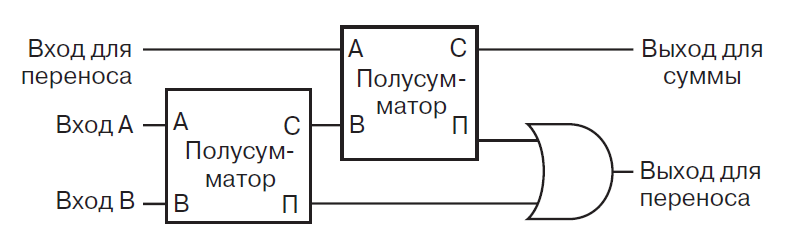
и получим полноценный сумматор

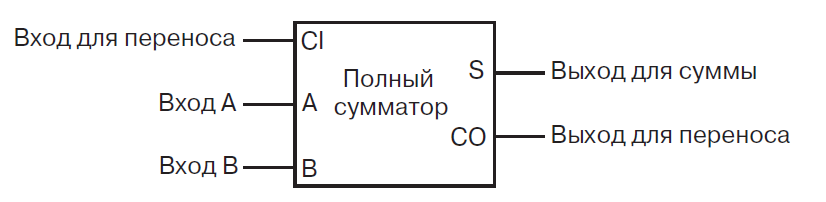
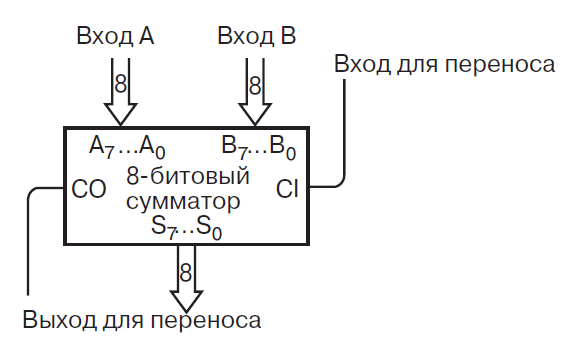
Соединив последовательно сумматоры в пакеты, например, по восемь, мы получим восьмибитный сумматор

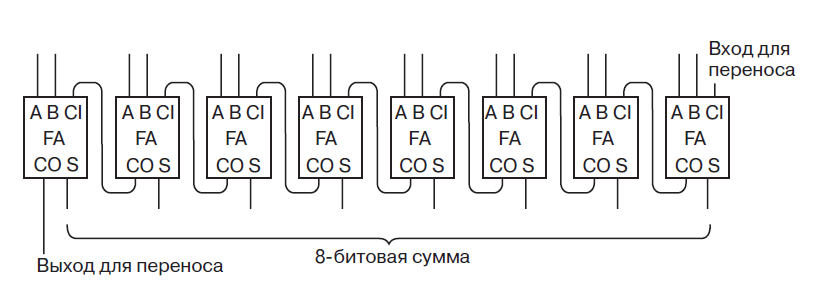
Перегруппируем входы и выходы

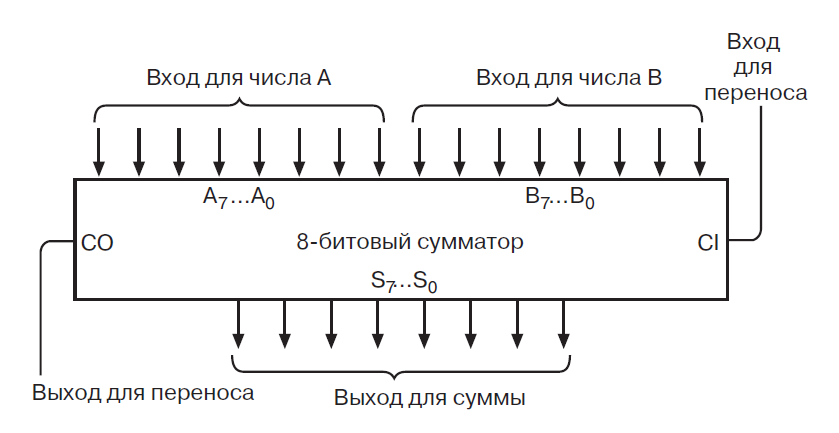
Эти сумматоры тоже можно соединять последовательно.

Два восьмибитных сумматора обеспечат работу с числами в диапазоне от $0$ до $2^{16}-1$, т.е. от $0$ до $65535$.

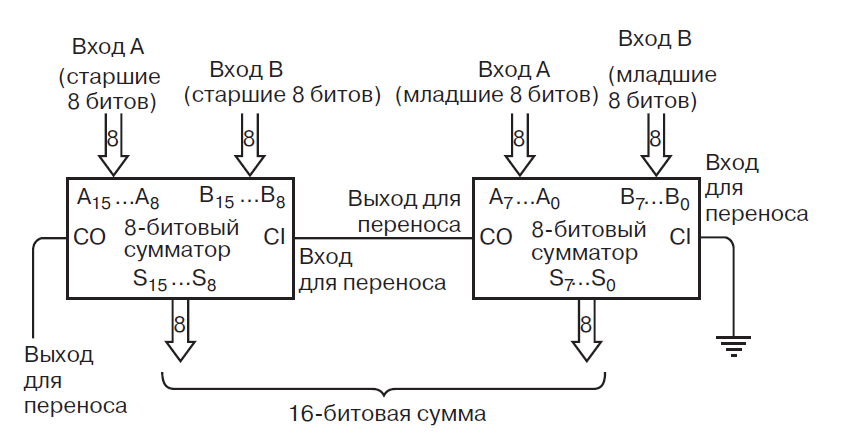
Это уже вполне полезная вычислительная машина, причём её можно собрать хоть на транзисторах, хоть на логических элементах (они продаются в магазинах радиодеталей, как и многие другие полезные микросхемы) с нуля.

Теория множеств

Исключающее ИЛИ полезно не только в построении логических схем, но и при работе с теорией множеств логики. Если мы возьмём аналогом суммы не объединение, а xor, тогда все операции будут полностью эквивалентны. Именно поэтому его ещё называют сложением по модулю два.

Обратный код

Вычитание в общем виде - довольно трудоёмкая задача. Нам постоянно нужно помнить, у каких разрядов мы занимали. Да, на бумажке это несложно, но нам ведь нужно собрать логическую схему вычитания. Хоть и в двоичной системе, это всё равно будет непросто.

Поэтому мы схитрим: пусть нам даны два числа $a$ и $b$, и бОльшее из них по модулю имеет $n$ разрядов в двоичном представлении. Тогда меньшее из них тоже будет иметь не больше $n$ разрядов.

Докажем от обратного наше утверждение, что если у наибольшего числа в двоичном представлении $n$ разрядов, то и у наименьшего будет не больше $n$. Пусть у наименьшего числа больше, чем $n$ разрядов. Тогда все разряды, большие $n$, будут вносить вклад в десятичное представление числа гарантированно больший, чем любое число записанное в двоичной системе счисления при помощи $n$ разрядов.

Вернёмся к вычитанию. Не теряя общности, назначим $a$ наибольшим по модулю. Если при этом разность должна получиться отрицательной, просто поменяем местами переменные до нашей логической схемы, а после инвертируем выход. Поэтому дальше мы будем рассматривать один конкретный случай вычитания $a-b$, где $a>b$ и при этом $a$ имеет $n$ разрядов в двоичном представлении. Все остальные случаи сводятся простыми преобразованиями к этому. Введём число $U=2^n$, в двоичном представлении состоящее из единицы в начале и $n$ нулей после. Также введём число $L=U-1$.

Вычитать нам придётся в любом случае, но мы можем разбить это вычитание на два очень простых.

$$a-b=a-b+U-U\\ a-b=a-b+L+1-U\\ a-b=a-b+U-U a-b=a-b+L+1-U a-b=a+(L-b)+1-U$$

$U$ очень удобно вычитать, это просто единица и куча нулей. Причём единица однозначно стоит у самого старшего разряда. Поэтому $U$ говорит нам просто о том, что нужно сделать со старшим разрядом.

Из $L$ вычесть заданное число тоже будет легко, потому что L полностью состоит из единиц. Число $(L-b)$ называют дополнительным кодом. Этот код как бы дополняет исходное число до максимального с таким же количеством разрядов. Дополнительный код на самом деле определён в системах с произвольным основанием, но в них он считается довольно трудоёмко, а вот в двоичной обратный код получить довольно просто, нам нужно всего лишь обратить каждый бит числа на противоположный. Это называется обратный код.

Рассмотрим вычитание на конкретном примере.

Записав эти числа в двоичном представлении, получаем задачу вида:

Вычтем вычитаемое из $11111111$(т.е. $255$)

Теперь складываем дополнение вычитаемого до 1 с уменьшаемым

Прибавляем к результату 1

Вычитаем $100000000$(т.е. $256$)

Число $1001101_{2}$ равно $77_{10}$.

Такую логическую схему реализовать гораздо проще. Правда, при этом диапазон значений смещается на половину своего размера в отрицательную сторону. Например, если диапазон неотрицательных чисел был от $0$ до $255$, то просто целые числа будут храниться в диапазоне от $-128$ до $127$.

Есть и более сложные операции. Например, умножение, взятие логарифма, корня. Для выполнения таких операций в современные процессоры добавляют специализированные микросхемы и даже сопроцессоры.

Память

Чтобы процессор выполнял те или иные команды, необходимо как-то сообщать ему о своих намерениях.

Машина Тьюринга

В нашем распоряжении есть логические элементы и регистры памяти. Их мы точно можем изготовить условно бесконечное количество. Возникает вопрос: любую ли задачу можно решить с помощью микросхем? Первым математически строго это сформулировал Алан Тьюринг.

Он предложил воображаемую виртуальную логическую машину, устроенную следующим образом. Вся информация, необходимая для работы устройства записана в ячейках бесконечной ленты. Исполнитель читает значение из стартовой ячейки, а дальше в зависимости от команды он может или записать новое значение в ту или иную ячейку, или прочитать новое.

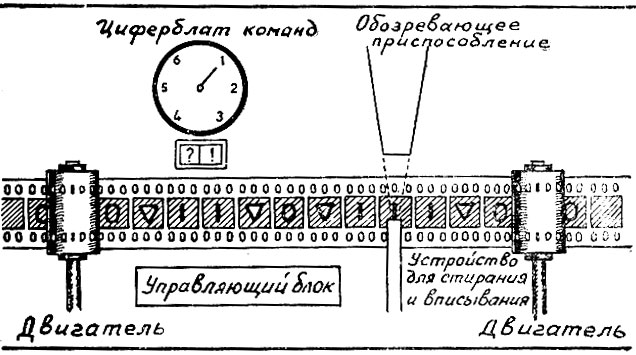
По умолчанию исполнитель просто перемещается от ячейки к ячейке.

Тезис Чёрча-Тьюринга

Хотя строгое доказательство тезиса до сих пор не разработано, всё развитие вычислительной техники показывает его справедливоcть. Т.к. это заключение чисто эмпирическое, то оно и называется тезисом. Звучит этот тезис так:

Всякий алгоритм может быть задан в виде соответствующей машины Тьюринга или частично рекурсивного определения, а класс вычислимых функций совпадает с классом частично рекурсивных функций и с классом функций, вычислимых на машинах Тьюринга

Если переводить этот тезис на язык физики, то любую задачу мы можем решить с помощью того или иного соединения транзисторных элементов.

Архитектура фон Неймана

Тем не менее машина Тьюринга была абсолютно абстрактной конструкцией. Первую практическую модель вычислительной машины предложил Джон фон Нейман. Логические модели вычислительных устройств называют архитектурой.

Современная архитектура компьютеров является продолжением идей фон Неймана, поэтому заслуженно называется его именем.

Суть архитектуры фон Неймана заключается в разделении вычислительного устройства на модули, каждый из которых решает конкретную, в первую очередь физическую, задачу.

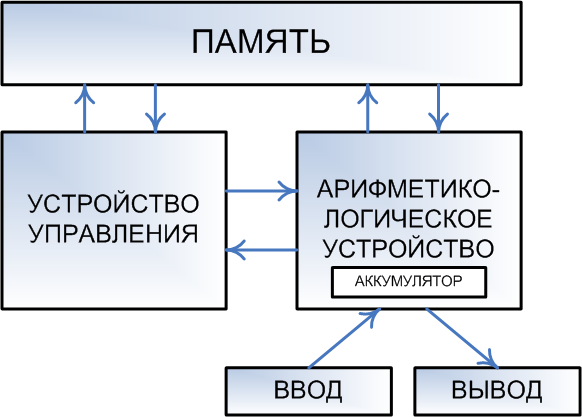
Его вычислительное устройство состояло из блока памяти, который хранил всю информацию, необходимую для работы вычислительной машины, арифметическо-логического устройства, иными словами процессора и устройства управления. Дополнительно в модель включены устройства ввода и вывода, ведь без них мы бы не смогли управлять преобразованиями информации и получать их результаты.

Фон Нейман первым предложил принцип однородности памяти. Согласно ему, между командами процессору и просто данными, нет никакой разницы с точки зрения механизма чтения. Вся разница проявляется при обработке прочитанного значения.

Исполнитель фон Неймана по сути не отличается от исполнителя Тьюринга. Фон нейман просто уточнил, что нужна не бесконечная лента, а физическое, конечное устройство хранения информации. Также он описал, как именно должны быть устроены ячейки памяти.

Не вдаваясь в подробности, суть сводится к тому, что каждая ячейка памяти состоит из $8$ бит. Каждая ячейка пронумерована и имеет свой адрес. Т.к. это новая величина, то была введена и новая единица измерения: байт.

$1$ байт равен $8$ битам.

Адресация

Такой размер ячейки выбран неслучайно. Ведь адрес нужно тоже нужно где-то хранить, это значит, что он должен помещаться в ячейку памяти. Выбор размера ячейки в битах обусловлен именно вопросом адресации.

Хотя первый микропроцессор Intel 4004, выпущенный в 1971 году, был 4-битным(рисунок ниже), быстро стало понятно, что 4 бита хранят слишком мало адресов.

Максимальное значение адреса, которое может хранить такая ячейка равно $2^4$, т.е. $16$. Это означает, что всего в памяти можно было бы хранить $16$ ячеек, каждая размером в $4$ бита. В итоге в такую память можно было записать $16*4=64$ бита информации.

Поэтому практически сразу был выпущен $8$-битный процессор Intel 8008.

Хотя разрядность увеличилась всего вдвое, это дало качественный скачок в ёмкости памяти. Ведь при $8$ битах в ячейке может поместиться число вплоть до $2^8=256$. Это значит, что ячеек памяти может быть $256$, к тому же каждая ячейка хранит по $8$ бит.

В дальнейшем увеличение разрядности процессора до 16 бит было неоправданно дорогостоящим, поэтому повышали разрядность только при работе с оперативной памятью. Вместо одного регистра памяти, работало два: один читал старший байт памяти, второй - младший. Такой подход впервые был реализован в процессоре Intel 8080.

Хотя в дальнейшем были освоены технологии производства процессоров с 16 разрядами регистров, а после и с 32 и 64, 8 бит стали частью массовой культуры не только как единица измерения байт, но и как игры, музыка и даже изобразительное искусство.

Если на любой тип информации у нас отводит только 8 бит, это означает, что все возможные цвета задаются этими восьмью битами, все музыкальные ноты и тональности.

Хотя довольно быстро появились микропроцессоры с $16$ разрядами, в игровых приставках долгое время использовались только $8$-битные процессоры, что и породило культуру $8$ бит.

Подробнее о развитии микропроцессоров можно почитать здесь.

Современным стандартом считается архитектура x64. Это означает, что каждый регистр состоит из 64 бит. Это означает, что присвоить адресы мы можем примерно 8192 гигабайтам или примерно 8 террабайт. Если нам нужен носитель размера побольше, то он просто разделяется на регионы, и как первые 16 битные системы хранения памяти ждёт от регистров два значения: номер региона и адрес внутри него.

Хотя такой же подход можно было делать и для меньших разрядностей, он сильно замедляет оперативную память, поэтому на регионы обычно делят только носители постоянной информации.

Основной из принципов компьютерной памяти заключается в том, что чем большее количество ячеек нам нужно уместить в замкнутом объёме, тем медленнее она работает. Одним из обязательных условий работы быстродействующей памяти(оперативной) является её зависимость от питания. Как только оно исчезает, все накопленные значения исчезают.

8 террабайт для оперативной памяти считаются достаточными для любого класса задач. Поэтому адрес скорее всего так и останется 64-битным, а вот для вычислений в современные процессоры добавляются специальные 128-битные регистры.

Assembler

В дальнейшем мы не будем рассматривать логические схемы, обеспечивающие выполнение тех или иных команд. Нас будут интересовать только их названия и логика выполнения. Подробнее о логических схемах организации оперативной памяти и других элементов можно прочитать в книге Чарьлза Пецрольда "Код". Скачать её можно здесь.

Не вдаваясь в подробности, работу современного процессора можно представить так: процессор читает первую ячейку памяти, начиная с которой помещается последовательность команд. Содержимое ячеек называется машинным словом, а сама последовательность - машинным кодом.

Регистр, в котором хранится адрес следующей команды в оперативной памяти, называется счётчиком команд.

Пока что мы будем считать, что все команды выполняются последовательно и никаких переходов не существует.

Важно понимать, что процессор принимает в качестве команд значения той или иной разрядности, иными словами числа. Эти числа-коды процессор сопоставляет с внутренними инструкциями и выполняет нужную команду.

Первые программы писались такими кодами. Чтобы занести их в оперативную память, использовались перфокарты.

Они не были изобретены специально для компьютеров. Изначально они служили в качестве шаблонов для рисунков ткацких станков. Подробнее можно почитать здесь.

С новой задачей они справлялись довольно качественно, но процесс их изготовления был слишком трудоёмким, и поэтому спустя несколько десятилетий был разработан монитор. Он позволял исправлять ошибки в машинных кодах и не тратить время на подготовку перфокарт. К тому же качественно возросла читаемость кода. Подробнее можно прочитать здесь.

На рисунке изображён 32-разрядный персональный компьютер DEC. Он был выпущен в 1978 году. Обратите внимание: справа в него вставляется кассета.

Внутри таких кассет расположено две катушки, на которых намотана магнитная лента. Когда наматывается одна катушка, вторая разматывает и наоброт.

До изобретения жётских дисков кассеты были самым распространённым постоянным носителем информации. Участки магнитной ленты с равным шагом намагничивались особым образом при записи, а при чтении эта остаточная намагниченность просто измерялась.

Когда появились первые мониторы, стало понятно, что машинный код - не лучший способ записи команд на экране. Было решено заменить машинные коды, состоящие из нулей и единиц буквенными командами и значениями, записанными в десятичной системе счисления. Эти команды образовали первый язык программирования Assembler (в переводе с английского транслятор).

У современных процессоров Intel, работающих в персональных компьютерах довольно много регистров, они делятся на группы по выполняемым функциям. В этом курсе мы рассмотри только группу регистров общего назначения: EAX, EBX, ECX, EDX. Подробнее о назначении регистров можно прочитать здесь.

Их всего 4, в каждый из них с помощью специальных команд мы можем поместить те или иные значения из оперативной памяти и, выполняя ту или иную команду, процессор будет брать из них данные, преобразовывать и сохранять в первый.

Рассмотрим команду сложения значений из регистров EAX и EBX. Чтобы её выполнить, процессор берёт числа из двух регистров EAX и EBX, а результат сложения помещает обратно в регистр EAX.

Важно понимать, что хотя названия и количество регистров общего назначения стали общепринятыми, тем не менее сама команда зависит от архитектуры процессора. Архитектура процессора - это система управляющих команд. Об этом подробнее будет рассказано в следующей главе.

Для архитектуры Pentium эта команда в численных кодах записывается как $01D8_{16}=111011000_2$. Размер одной ячейки памяти равен $1$ байт, в шестнадцатеричной систем все значения, помещающиеся в одном байте можно записать с помощью двух шестнадцатеричных символов. Значит, команда суммы занимает два байта.

Для других архитектур та же самая команда может иметь другой код и даже другой размер. Основная сила ассемблера заключается в том, что под каждую платформу написана своя версия интерпретатора. Основные команды записываются одинаково, отличие заключается только в архитектурнозависимых тонкостях. Нужно просто установить копилятор для той или иной архитектуры, и он перевёдт наши исходники на ассемблере в машинный код, нужного формата.

Это означает, что простые программы с помощью ассемблера простые можно написать один раз и потом запускать на всех платформах. На языке assembler рассмотренная команда суммы записывается так:

add eax, ebx

Каждая команда ассемблера начинается с новой строчки. Первым словом идёт название команды, потом через запятую перечисляются её аргументы.

Чтобы запустить программу на ассемблере, нужно запустить транслятор её в машинные коды, который у каждой архитектуры свой, после чего записать их в исполняемый файл. Хотя основные команды не зависят от операционной системы, прикладные решения зависят от платформы. Поэтому зачастую приходится писать отдельную программу на той или иной версии ассемблера, предназначенного для работы на конкретной операционной системе.

Подробнее про программирование на языке assembler можно прочитать в книге Столярова А.В. "Программирование на языке ассемблера NASM для ОС UNIX". Скачать её можно здесь.