Примитивы

Теоретический блок

В этом блоке описаны все примитивы и как написать приложение для их демонстрации, вам нужно разобраться только с рисованием примитивов, нужных в вашем задании

Для тестов примитивов напишем новую программу. По клавишам "влево" и "вправо" будем переходить к предыдущему или следующему примитиву соответственно.

example

Исходники этого приложения можно скачать здесь

Из предыдущих проектов нам понадобятся классы Panel и GridPanel, а также пакет misc.

example

Класс Application нужно переписать:

Application.java

package app;

import io.github.humbleui.jwm.*;
import io.github.humbleui.jwm.skija.EventFrameSkija;
import io.github.humbleui.skija.Canvas;
import io.github.humbleui.skija.Surface;
import misc.CoordinateSystem2i;
import misc.Misc;
import panels.PanelPrimitives;

import java.io.File;
import java.util.function.Consumer;

/**
 * Класс окна приложения
 */
public class Application implements Consumer<Event> {
    /**
     * цвет фона
     */
    public static final int APP_BACKGROUND_COLOR = Misc.getColor(255, 38, 70, 83);

    /**
     * окно приложения
     */
    private final Window window;
    /**
     * отступ приложения
     */
    public static final int PANEL_PADDING = 5;
    /**
     * радиус скругления элементов
     */
    public static final int C_RAD_IN_PX = 4;

    /**
     * Панель информации
     */
    private final PanelPrimitives panelPrimitives;

    /**
     * Конструктор окна приложения
     */
    public Application() {
        // создаём окно
        window = App.makeWindow();

        // панель игры
        panelPrimitives = new PanelPrimitives(window, false, APP_BACKGROUND_COLOR, PANEL_PADDING);

        // задаём обработчиком событий текущий объект
        window.setEventListener(this);
        // задаём заголовок
        window.setTitle("Java 2D");
        // задаём размер окна
        window.setWindowSize(900, 900);
        // задаём его положение
        window.setWindowPosition(100, 100);

        // задаём иконку
        switch (Platform.CURRENT) {
            case WINDOWS -> window.setIcon(new File("src/main/resources/windows.ico"));
            case MACOS -> window.setIcon(new File("src/main/resources/macos.icns"));
        }

        // названия слоёв, которые будем перебирать
        String[] layerNames = new String[]{
                "LayerGLSkija", "LayerRasterSkija"
        };

        // перебираем слои
        for (String layerName : layerNames) {
            String className = "io.github.humbleui.jwm.skija." + layerName;
            try {
                Layer layer = (Layer) Class.forName(className).getDeclaredConstructor().newInstance();
                window.setLayer(layer);
                break;
            } catch (Exception e) {
                System.out.println("Ошибка создания слоя " + className);
            }
        }

        // если окну не присвоен ни один из слоёв
        if (window._layer == null)
            throw new RuntimeException("Нет доступных слоёв для создания");

        // делаем окно видимым
        window.setVisible(true);
    }

    /**
     * Обработчик событий
     *
     * @param e событие
     */
    @Override
    public void accept(Event e) {
        // если событие - это закрытие окна
        if (e instanceof EventWindowClose) {
            // завершаем работу приложения
            App.terminate();
            // закрытие окна
        } else if (e instanceof EventWindowCloseRequest) {
            window.close();
        } else if (e instanceof EventFrameSkija ee) {
            Surface s = ee.getSurface();
            paint(s.getCanvas(), new CoordinateSystem2i(0, 0, s.getWidth(), s.getHeight())
            );
        } else if (e instanceof EventFrame) {
            // запускаем рисование кадра
            window.requestFrame();
        }  else if (e instanceof EventKey eventKey) {
            if (eventKey.isPressed()) {
                switch (eventKey.getKey()) {
                    case ESCAPE -> window.close();
                }
            }
        }

    }

    /**
     * Рисование
     *
     * @param canvas   низкоуровневый инструмент рисования примитивов от Skija
     * @param windowCS СК окна
     */
    public void paint(Canvas canvas, CoordinateSystem2i windowCS) {
        // запоминаем изменения (пока что там просто заливка цветом)
        canvas.save();
        // очищаем канвас
        canvas.clear(APP_BACKGROUND_COLOR);
        // рисуем панели
        panelPrimitives.paint(canvas, windowCS);
        canvas.restore();
    }
}

Чтобы упростить работу с примитивами, в пакете app определим функциональный интерфейс примитива Primitive и вместо кучи классов для каждого примитива будем добавлять анонимный класс с реализацией рисования конкретного примитива.

Primitive.java

package app;

import io.github.humbleui.skija.Canvas;
import io.github.humbleui.skija.Paint;
import misc.CoordinateSystem2i;

/**
 * Функциональный интерфейс примитива
 */
public interface Primitive {
    /**
     * рисование
     *
     * @param canvas   область рисования
     * @param windowCS СК окна
     * @param p        перо
     */
    void render(Canvas canvas, CoordinateSystem2i windowCS, Paint p);
}

PanelPrimitives.java

package panels;

import app.Primitive;
import io.github.humbleui.jwm.Event;
import io.github.humbleui.jwm.EventKey;
import io.github.humbleui.jwm.Window;
import io.github.humbleui.skija.Canvas;
import io.github.humbleui.skija.Paint;
import io.github.humbleui.skija.RRect;
import misc.CoordinateSystem2i;
import misc.Misc;

import java.util.ArrayList;

/**
 * Панель игры
 */
public class PanelPrimitives extends Panel {
    /**
     * Список примитивов
     */
    private final ArrayList<Primitive> primitives = new ArrayList<>();
    /**
     * Положение текущего примитива
     */
    private int primitivePos;

    /**
     * Конструктор панели
     *
     * @param window          окно
     * @param drawBG          нужно ли рисовать подложку
     * @param backgroundColor цвет фона
     * @param padding         отступы
     */
    public PanelPrimitives(Window window, boolean drawBG, int backgroundColor, int padding) {
        super(window, drawBG, backgroundColor, padding);
        // добавляем точку
        primitives.add(((canvas, windowCS, p) -> canvas.drawRRect(
                RRect.makeXYWH(200, 200, 4, 4, 2), p)
        ));
        primitivePos = 0;
    }

    /**
     * Обработчик событий
     *
     * @param e событие
     */
    @Override
    public void accept(Event e) {
        // кнопки клавиатуры 
        if (e instanceof EventKey eventKey) {
            // кнопка нажата с Ctrl
            if (eventKey.isPressed()) {
                 switch (eventKey.getKey()) {  
                    // Следующий примитив
                    case LEFT -> primitivePos = (primitivePos - 1 + primitives.size()) % primitives.size();
                    // Предыдущий примитив
                    case RIGHT -> primitivePos = (primitivePos + 1) % primitives.size();
                 }
            }
        }
    }    


    /**
     * Метод под рисование в конкретной реализации
     *
     * @param canvas   область рисования
     * @param windowCS СК окна
     */
    @Override
    public void paintImpl(Canvas canvas, CoordinateSystem2i windowCS) {
        // создаём перо
        Paint p = new Paint();
        // задаём цвет
        p.setColor(Misc.getColor(200, 255, 255, 255));
        // задаём толщину пера
        p.setStrokeWidth(5);
        // рисуем текущий примитив
        primitives.get(primitivePos).render(canvas, windowCS, p);
    }


}

Теперь добавим обработку событий панелью примитивов accept() в обработчике событий класса Aplication

        ...
        // запускаем обработку событий у панели примитивов
        panelPrimitives.accept(e);
        ...

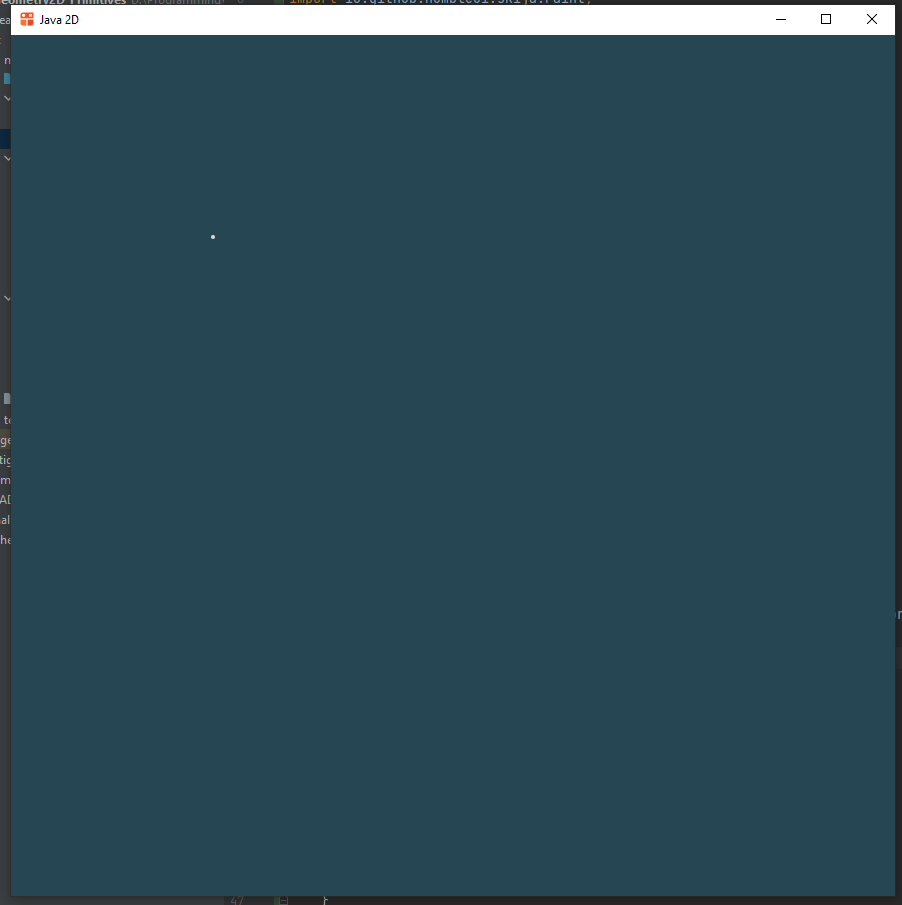
Точка

Точка Задается своими координатами $x$ и $y$ . Чтобы нарисовать точку, используйте команду

    canvas.drawRRect(RRect.makeXYWH(x-2, y-2, 4, 4, 2), p)))

Сама команда рисования - это canvas.drawRect(), она принимает в качестве аргумента скруглённый квадрат. Квадрат создаётся командой-фабрикой RRect.makeXYWH(). Эта команда в качестве аргументов принимает положение квадрата по оси x, по оси y, его ширину, высоту и радиус скеругления.

Поэтому, чтобы создать точку с центром в $[x,y]$ , нужно при передаче в аргументы фабрики положения, надо из каждой из его координат вычесть половину размера прямоугольника, в нашем случае половина ширины равна половине высоты и равна двум.

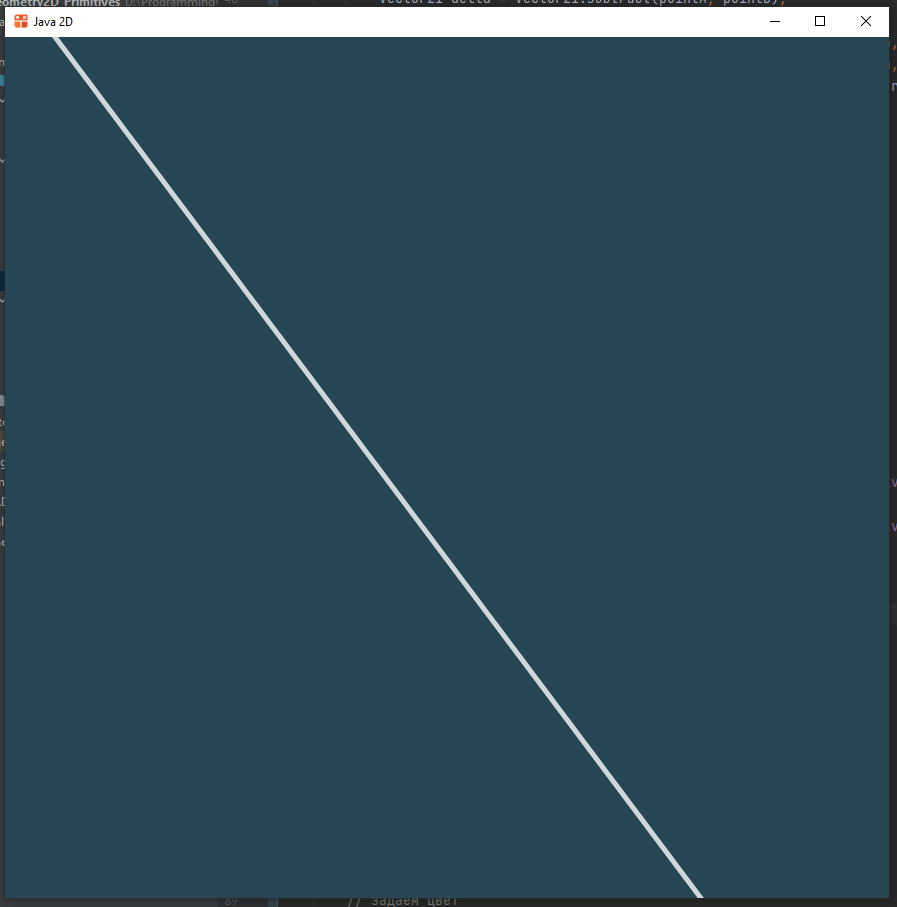
example

Прямая

Прямая задается двумя точками, через которые проходит.

Для начала нам понадобится метод умножения целочисленного вектора на число. Добавим его в класс Vector2i:

    /**
     * Умножение вектора на число
     *
     * @param v вектор
     * @param s число
     * @return результат умножения
     */
    public static Vector2i mult(Vector2i v, int s) {
        return new Vector2i(v.x * s, v.y * s);
    }

У движка нет готового метода рисования линий, потому что линия - бесконечный объект, но у него есть метод рисования отрезка canvas.drawLine(). В качестве аргументов он принимает сначала координаты первой точки, потом второй, пятый аргумент - это перо.

Чтобы нарисовать именно линию, нам нужно продлить данный нам отрезок в обе стороны так, чтобы оба его конца выходили за границы экрана. Тогда линия точно нарисуется во весь экран.

Для этого просто найдём вектор, который ведёт из точки A в точку B, умножим его на длину диагонали экрана. Тогда, чтобы получить первую опорную точку, нам нужно прибавить этот вектор к точке A, а чтобы вторую - вычесть.

В конструкторе добавим новый примитив

        // добавляем линию
        primitives.add((canvas, windowCS, p) -> {
            // опорные точки линии
            Vector2i pointA = new Vector2i(200, 200);
            Vector2i pointB = new Vector2i(500, 600);
            // вектор, ведущий из точки A в точку B
            Vector2i delta = Vector2i.subtract(pointA, pointB);
            // получаем максимальную длину отрезка на экране, как длину диагонали экрана
            int maxDistance = (int) windowCS.getSize().length();
            // получаем новые точки для рисования, которые гарантируют, что линия
            // будет нарисована до границ экрана
            Vector2i renderPointA = Vector2i.sum(pointA, Vector2i.mult(delta, maxDistance));
            Vector2i renderPointB = Vector2i.sum(pointA, Vector2i.mult(delta, -maxDistance));
            // рисуем линию
            canvas.drawLine(renderPointA.x, renderPointA.y, renderPointB.x, renderPointB.y, p);
        });
        primitivePos = 0;

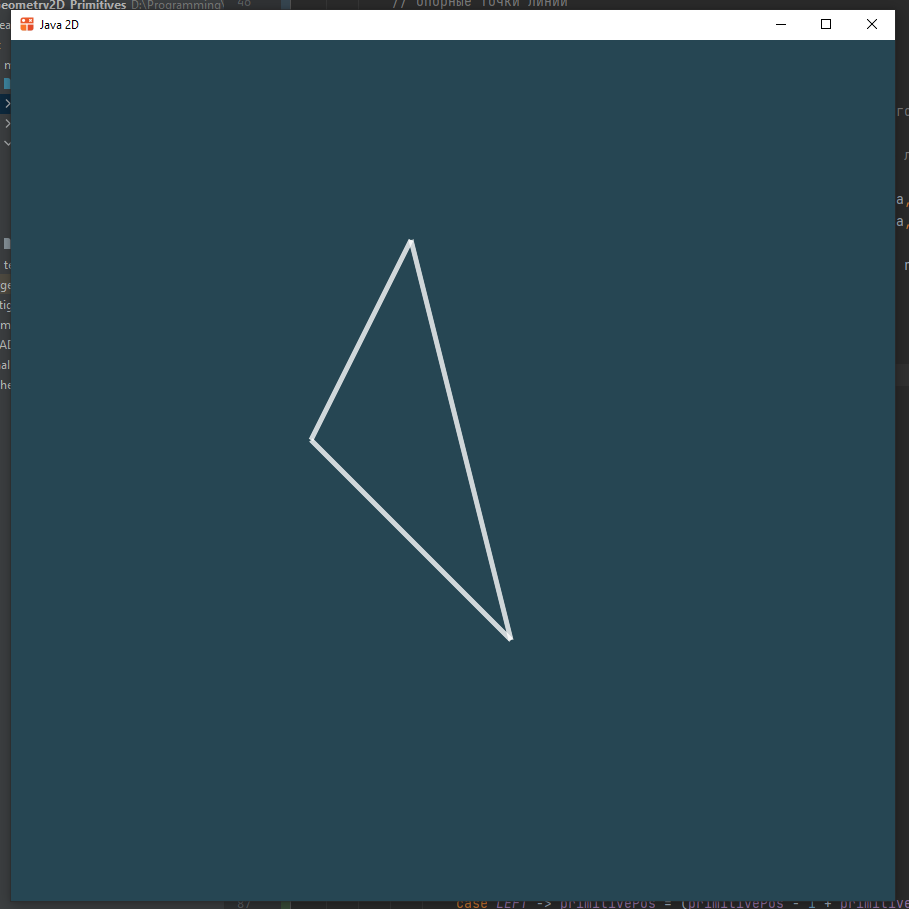
example

Треугольник

Треугольник задается тремя точками-вершинами, точки попарно не совпадают.

Чтобы нарисовать треугольник, нужно просто нарисовать три отрезка

        // добавляем треугольник
        primitives.add((canvas, windowCS, p) -> {
            // вершины треугольника
            Vector2i pointA = new Vector2i(400, 200);
            Vector2i pointB = new Vector2i(500, 600);
            Vector2i pointC = new Vector2i(300, 400);
            // рисуем его стороны
            canvas.drawLine(pointA.x, pointA.y, pointB.x, pointB.y, p);
            canvas.drawLine(pointB.x, pointB.y, pointC.x, pointC.y, p);
            canvas.drawLine(pointC.x, pointC.y, pointA.x, pointA.y, p);
        });

example

Окружность

Окружность задается точкой центра и точкой на окружности, точки не совпадают.

Т.к. окружность при решении задачи будет задаваться в СК задачи, а не экрана, то, скорее всего, при рисовании круг отобразится в эллипс, т.к. пропорции вдоль осей между СК экрана и СК задачи почти всегда не равны.

У движка есть готовая команда рисования эллипса canvas.drawOval(), в качестве аргумента она принимает объект класса Rect, т.е. эта команда работает так же, как canvas.drawRect(), но вместо прямоугольника она рисует вписанный в этот прямоугольник эллипс. Также есть команда нарисовать круг canvas.drawCircle(), в качестве аргументов она принимает x координату центра, y координату, радиус круга и перо.

Оба этих метода рисуют сплошные фигуры, но для решения геометрических задач нам нужно видеть как можно больше фигур, поэтому эллипс следует нарисовать с помощью прямых.

У движка есть готовый метод рисования набора отрезков canvas.drawLines(). Этому методу передать массив вещественных чисел float размером в четыре раза большим, чем кол-во линий. В этом массиве все данные идут подряд: сначала x координата первой точки, потом y координата, потом x координата второй точки, потом y координата, следующие четыре элемента точно также описывают второй отрезок и т.д.

Чтобы нарисовать эллипс, в частном случае окружность, нам нужно перебрать углы от $0$ до $2\pi$ с небольшим шагом. Из этих углов с помощью синусов и косинусов мы получим координаты этих точек, а потом просто заполним ими массив. У круга синус и косинус рассматриваемого угла домножаются на один и тот же радиус, а у эллипса на соответствующие радиус вдоль оси y и на радиус оси x соответственно.

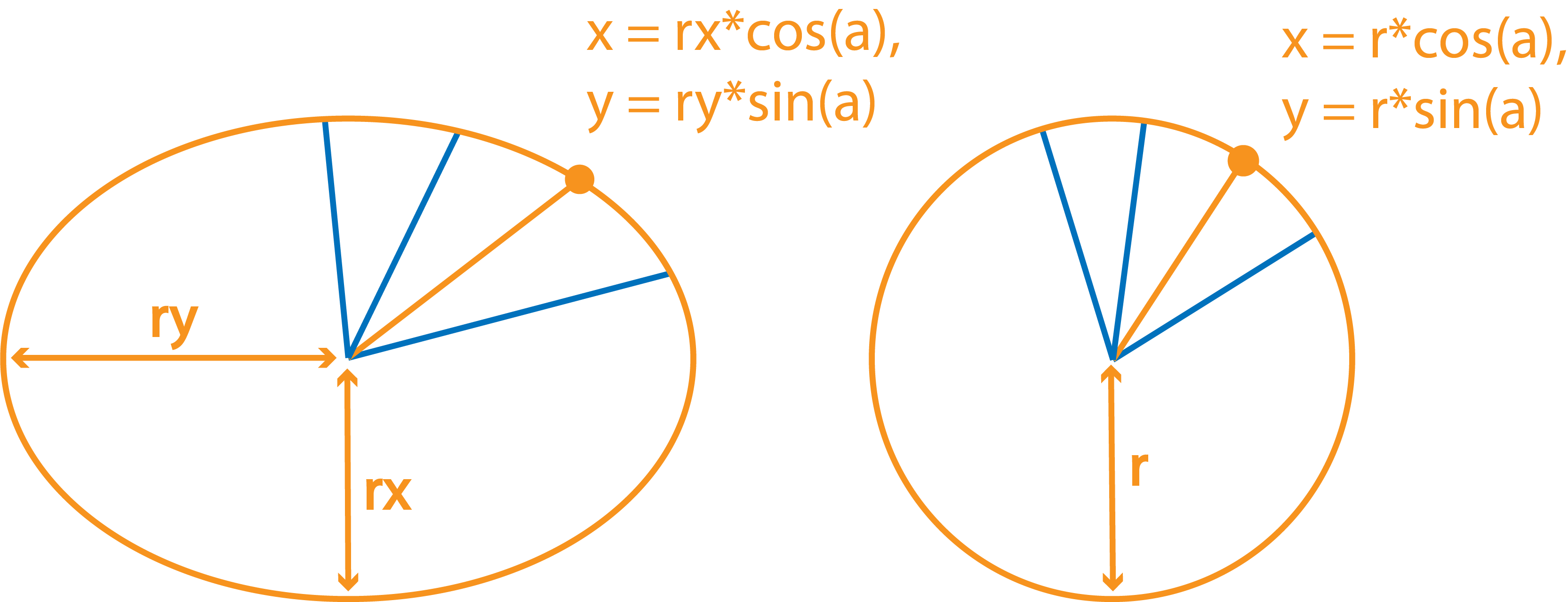
example

Добавим теперь примитив окружности

        // добавляем окружность
        primitives.add((canvas, windowCS, p) -> {
            // центр окружности
            Vector2i center = new Vector2i(350, 350);
            // радиус окружности
            int rad = 200;
            // радиус вдоль оси x
            int radX = (int) (rad * 1.3);
            // радиус вдоль оси y
            int radY = (int) (rad * 0.9);
            // кол-во отсчётов цикла
            int loopCnt = 40;
            // создаём массив координат опорных точек
            float[] points = new float[loopCnt * 4];
            // запускаем цикл
            for (int i = 0; i < loopCnt; i++) {
                // x координата первой точки
                points[i * 4] = (float) (center.x + radX * Math.cos(Math.PI / 20 * i));
                // y координата первой точки
                points[i * 4 + 1] = (float) (center.x + radY * Math.sin(Math.PI / 20 * i));

                // x координата второй точки
                points[i * 4 + 2] = (float) (center.x + radX * Math.cos(Math.PI / 20 * (i + 1)));
                // y координата второй точки
                points[i * 4 + 3] = (float) (center.x + radY * Math.sin(Math.PI / 20 * (i + 1)));
            }
            // рисуем линии
            canvas.drawLines(points, p);

        });

Программа теперь нарисует нам эллипс, если перейти к этому режиму

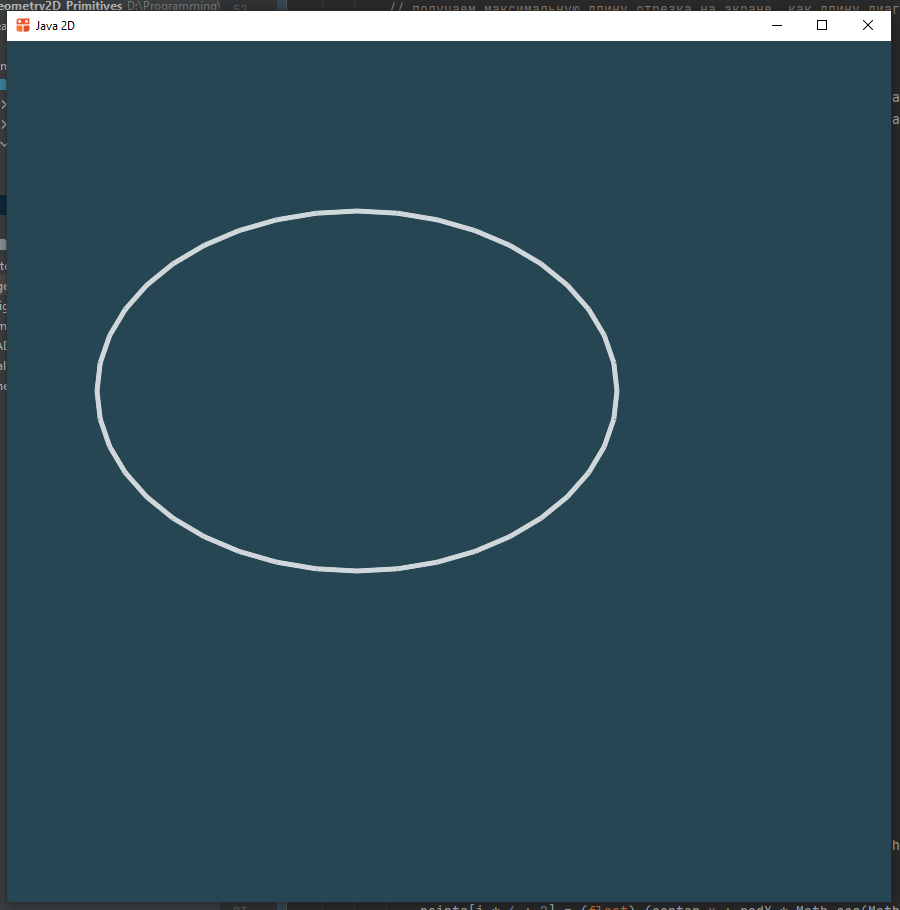
example

Параллельный прямоугольник

Параллельный прямоугольник задается точками двумя противоположными вершинами. Все стороны параллельны осям координат, координаты вершин не совпадают по каждой из координат.

Чтобы нарисовать параллельный прямоугольник, нам достаточно просто нарисовать четыре линии:

        // добавляем параллельный прямоугольник
        primitives.add((canvas, windowCS, p) -> {
            // левая верхняя вершина
            Vector2i pointA = new Vector2i(200, 100);
            // правая нижняя
            Vector2i pointC = new Vector2i(300, 500);

            // рассчитываем опорные точки прямоугольника
            Vector2i pointB = new Vector2i(pointA.x, pointC.y);
            Vector2i pointD = new Vector2i(pointC.x, pointA.y);

            // рисуем его стороны
            canvas.drawLine(pointA.x, pointA.y, pointB.x, pointB.y, p);
            canvas.drawLine(pointB.x, pointB.y, pointC.x, pointC.y, p);
            canvas.drawLine(pointC.x, pointC.y, pointD.x, pointD.y, p);
            canvas.drawLine(pointD.x, pointD.y, pointA.x, pointA.y, p);
        });

Прямоугольник

Прямоугольник задается двумя вершинами одной из сторон, а также точкой, лежащей на прямой, проходящей через две другие вершины.

Чтобы найти опорные точки прямоугольника, нам необходимо создать класс линии, а в нём прописать метод расстояния от точки до прямой.

Чтобы найти координаты опорных точек, нам понадобится функция поворота вектора на угол.

В рисовании этого примитива задействовано несколько векторных операций. Если мы будем работать с целочисленным вектором, то мы потеряем слишком много значащих чисел, поэтому все методы пропишем в вещественном векторе.

Для удобства пропишем конструктор вещественного вектора от целочисленного

    /**
     * Конструктор вектора создаёт нулевой вектор
     */
    public Vector2d(Vector2i v) {
        this.x = v.x;
        this.y = v.y;
    }

Также нам понадобится метод преобразования вещественного вектора в целочисленный

    /**
     * Получить целочисленный вектор
     *
     * @return целочисленный вектор
     */
    public Vector2i intVector() {
        return new Vector2i((int) x, (int) y);
    }

Для двумерного вектор поворот вычисляется по следующей формуле

x_r = x_0 \cos(a)-y_0 \sin(a)\\ y_r = x_0 \sin(a)+y_0 \cos(a)

где $[x_0, y_0]$ - координаты исходного вектора, $[x_r, y_r]$ - координаты повёрнутого, $a$ - угол, на который выполняется поворот.

    /**
     * Повернуть вектор
     *
     * @param a угол
     * @return повёрнутый вектор
     */
    public Vector2d rotated(double a) {
        return new Vector2d(
                x * Math.cos(a) - y * Math.sin(a),
                x * Math.sin(a) + y * Math.cos(a)
        );
    }

Также нам понадобится метод нормализации вектора. Нормализованный вектор - это вектор, сонаправленный с исходным, но имеющий единичную длину. Чтобы получить нормализованный вектор, нужно просто каждую из его координат разделить на длину.

    /**
     * Нормализация вектора
     *
     * @return нормированный вектор
     */
    public Vector2d norm() {
        double length = length();
        return new Vector2d(x / length, y / length);
    }

Ещё нам понадобится метод, возвращающий векторное произведение векторов. Строго говоря, для двумерного вектора оно не определено. Т.к. результат векторного умножения - это вектор.

Но для двумерного вектора придумана хитрость: мы создаём на основе исходных двумерных векторов трёхмерные, у которых координата $z$ равна нулю, тогда результатом их векторного умножения будет вектор, сонаправленный с осью $z$ . Т.е. длина этого вектора равна модулю $z$ координаты. Эта координата и берётся за результат векторного умножения двумерных векторов.

Обозначим результат векторного умножения за $v$ , а перемножаемые вектора за $a$ и $b$ , тогда умножение вычисляется по следующей формуле:

v = a\times b = a.x*b.y - a.y*b.x

Векторное умножение обозначается $\times$

Теперь напишем метод векторного умножения

    /**
     * Векторное умножение векторов
     *
     * @param v второй вектор
     * @return результат умножения
     */
    public double cross(Vector2d v) {
        return this.x * v.y - this.y * v.x;
    }

Он нам нужен для определения того, в какую сторону направить смещение.

Знак векторного произведения также определяет знак синуса угла между векторами. Нас интересует, куда следует повернуть вектор: по часовой стрелке или против часовой. Повороту по часовой стрелке соответствуют отрицательные углы, а против часовой - положительные.

Знак угла нам нужне, чтобы понять, куда направить вектор смещения $E$ . Вектор смещения - это вектор, прибавив который к координатам вершины $A$ мы получим координаты вершины $D$ , а к координатам $C$ - координаты вершины $D$ .

На диапазоне значений $[-\pi,\pi]$ знак синуса, т.е. знак векторного произведения совпадает со знаком угла. Получается, чтобы определить направление поворота вектора смещения, нам нужно просто определить знак угла между $\vec{AB}$ и $\vec{AP}$ .

Если этот угол положительный, то и угол между известной стороной и вектором смещения тоже будет положительным, а если угол отрицательный, то отрицательный.

Угол между вектором смещения и известной стороной можно найти по следующей формуле

e = sign(p)\frac{\pi}{2}=sign(\vec{AB}\times\vec{AD})\frac{\pi}{2}

$sign()$ - функция знака, возвращает $-1$ , если её аргумент отрицательный, $0$ - если он равен нулю и $1$ если положительный.

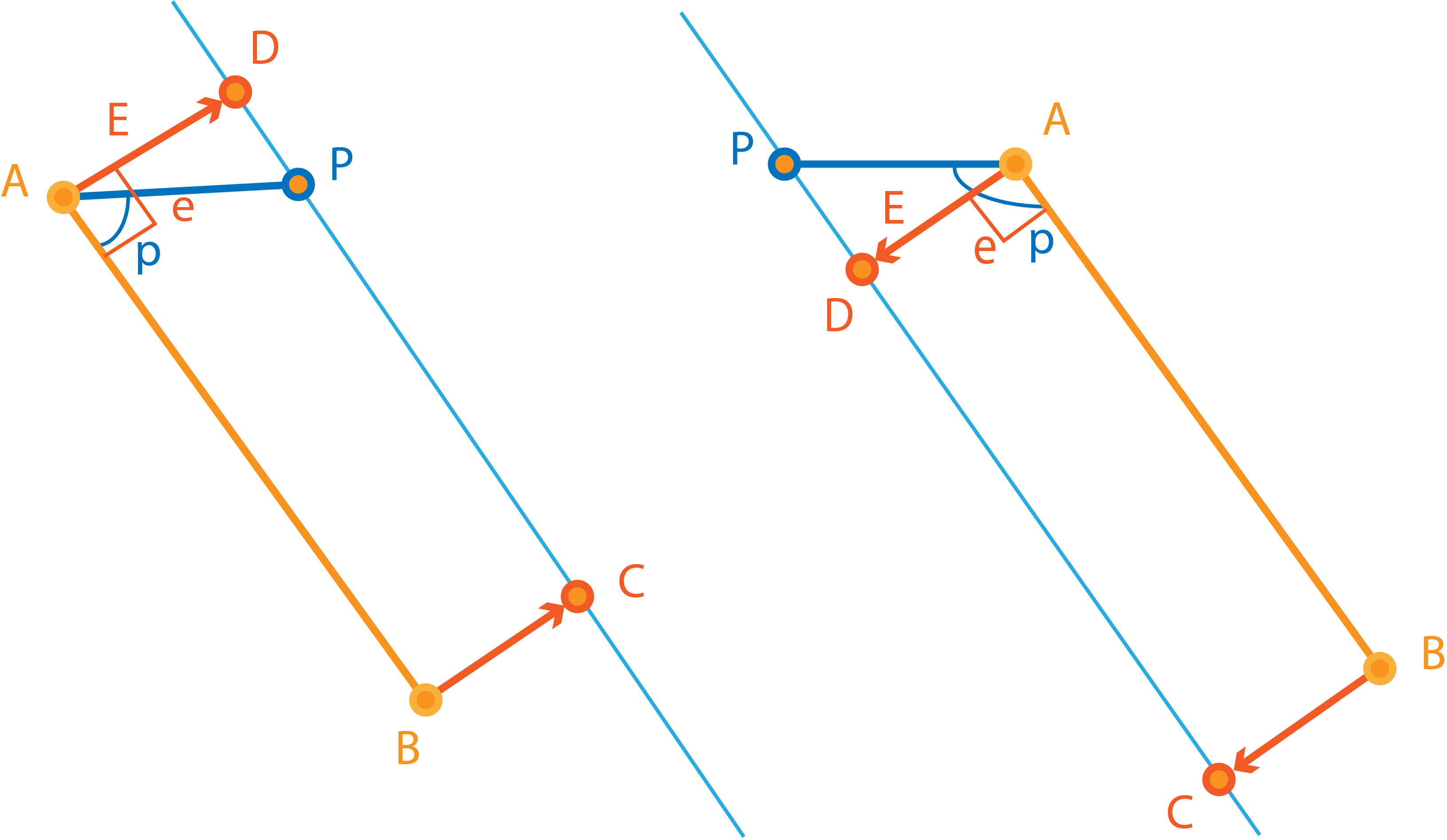
example

Если прямая определяется двумя точками $A(x_a, y_a)$ и $B(x_b, y_b)$ , то коэффициенты её канонического уравнения

ax + by + c = 0

Можно найти по формулам:

a = y_a - y_b \\ b = x_a - x_b \\ c = x_a y_b - x_b y_a

Расстояние от точки $P(x_0,y_0)$ до прямой $ax+by+c=0$ находится по формуле:

d = \frac{|ax_0+by0+c|}{\sqrt{a^2+b^2}}

Добавим класс Line в пакет app.

Line.java

package app;

import misc.Vector2d;

/**
 * Класс линии
 */
public class Line {
    /**
     * Первая опорная точка
     */
    private final Vector2d pointA;
    /**
     * Вторая опорная точка
     */
    private final Vector2d pointB;
    /**
     * Первый коэффициент канонического уравнения прямой
     */
    private final double a;
    /**
     * Второй коэффициент канонического уравнения прямой
     */
    private final double c;
    /**
     * Третий коэффициент канонического уравнения прямой
     */
    private final double b;

    /**
     * Конструктор линии
     *
     * @param pointA первая опорная точка
     * @param pointB вторая опорная точка
     */
    public Line(Vector2d pointA, Vector2d pointB) {
        this.pointA = pointA;
        this.pointB = pointB;

        a = pointA.y - pointB.y;
        b = pointB.x - pointA.x;
        c = pointA.x * pointB.y - pointB.x * pointA.y;
    }

    /**
     * Получить расстояние до точки
     *
     * @param pos координаты точки
     * @return расстояние
     */
    public double getDistance(Vector2d pos) {
        return Math.abs(a * pos.x + b * pos.y + c) / Math.sqrt(a * a + b * b);
    }
}

Теперь добавим сам примитив в конструкторе панели примитивов

        ...    
        // добавляем прямоугольник
        primitives.add((canvas, windowCS, p) -> {
            // первая вершина
            Vector2i pointA = new Vector2i(200, 100);
            // вторая вершина
            Vector2i pointB = new Vector2i(400, 300);
            // точка на противоположной стороне
            Vector2i pointP = new Vector2i(100, 300);
            // создаём линию
            Line line = new Line(new Vector2d(pointA), new Vector2d(pointB));
            // рассчитываем расстояние от прямой до точки
            double dist = line.getDistance(new Vector2d(pointP));
            // рассчитываем векторы для векторного умножения
            Vector2d AB = Vector2d.subtract(new Vector2d(pointB), new Vector2d(pointA));
            Vector2d AP = Vector2d.subtract(new Vector2d(pointP), new Vector2d(pointA));
            // определяем направление смещения
            double direction = Math.signum(AB.cross(AP));
            // получаем вектор смещения
            Vector2i offset = AB.rotated(Math.PI / 2 * direction).norm().mult(dist).intVector();

            // находим координаты вторых двух вершин прямоугольника
            Vector2i pointC = Vector2i.sum(pointB, offset);
            Vector2i pointD = Vector2i.sum(pointA, offset);

            // рисуем его стороны
            canvas.drawLine(pointA.x, pointA.y, pointB.x, pointB.y, p);
            canvas.drawLine(pointB.x, pointB.y, pointC.x, pointC.y, p);
            canvas.drawLine(pointC.x, pointC.y, pointD.x, pointD.y, p);
            canvas.drawLine(pointD.x, pointD.y, pointA.x, pointA.y, p);

            // сохраняем цвет рисования
            int paintColor = p.getColor();
            // задаём красный цвет
            p.setColor(Misc.getColor(200, 255, 0, 0));
            canvas.drawRRect(RRect.makeXYWH(pointA.x - 4, pointA.y - 4, 8, 8, 4), p);
            canvas.drawRRect(RRect.makeXYWH(pointB.x - 4, pointB.y - 4, 8, 8, 4), p);
            canvas.drawRRect(RRect.makeXYWH(pointP.x - 4, pointP.y - 4, 8, 8, 4), p);
            // восстанавливаем исходный цвет рисования
            p.setColor(paintColor);
        });
        ...

Для самоконтроля помимо самого прямоугольника добавлено рисование опорных точек.

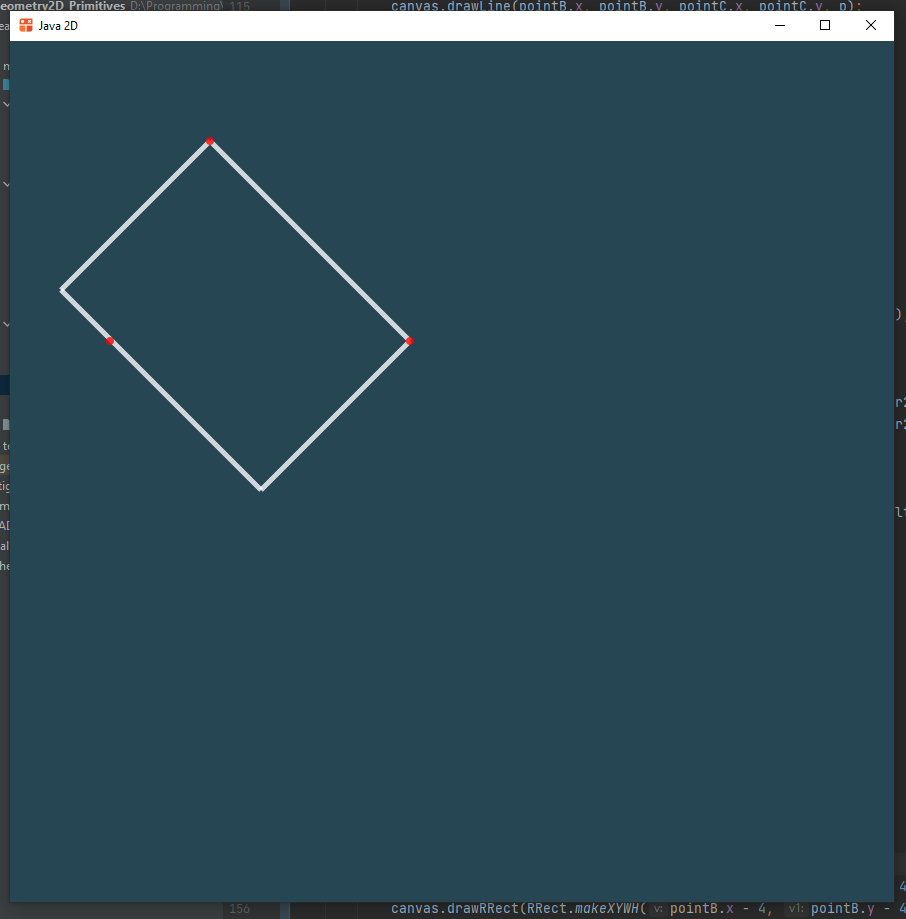
example

Параллелограмм

Задается тремя точками вершинами. Четвертая вершина определяется через три другие.

Пусть нам даны три вершины параллелограмма $A$ , $B$ и $C$ . Тогда координаты точки $D$ можно определить как $C+\vec{AB}$ .

Запишем это в коде:

        ...
        // добавляем параллелограмм
        primitives.add((canvas, windowCS, p) -> {
            // вершины треугольника
            Vector2i pointA = new Vector2i(200, 300);
            Vector2i pointB = new Vector2i(100, 100);
            Vector2i pointC = new Vector2i(300, 200);

            // определяем вектор смещения
            Vector2i AB = Vector2i.subtract(pointA, pointB);
            Vector2i pointD = Vector2i.sum(pointC, AB);

            // рисуем его стороны
            canvas.drawLine(pointA.x, pointA.y, pointB.x, pointB.y, p);
            canvas.drawLine(pointB.x, pointB.y, pointC.x, pointC.y, p);
            canvas.drawLine(pointC.x, pointC.y, pointD.x, pointD.y, p);
            canvas.drawLine(pointD.x, pointD.y, pointA.x, pointA.y, p);

            // сохраняем цвет рисования
            int paintColor = p.getColor();
            // задаём красный цвет
            p.setColor(Misc.getColor(200, 255, 0, 0));

            // рисуем опорные точки
            canvas.drawRRect(RRect.makeXYWH(pointA.x - 4, pointA.y - 4, 8, 8, 4), p);
            canvas.drawRRect(RRect.makeXYWH(pointB.x - 4, pointB.y - 4, 8, 8, 4), p);
            canvas.drawRRect(RRect.makeXYWH(pointC.x - 4, pointC.y - 4, 8, 8, 4), p);

            // восстанавливаем исходный цвет рисования
            p.setColor(paintColor);
        });
        ...

Получим рисование параллелограмма

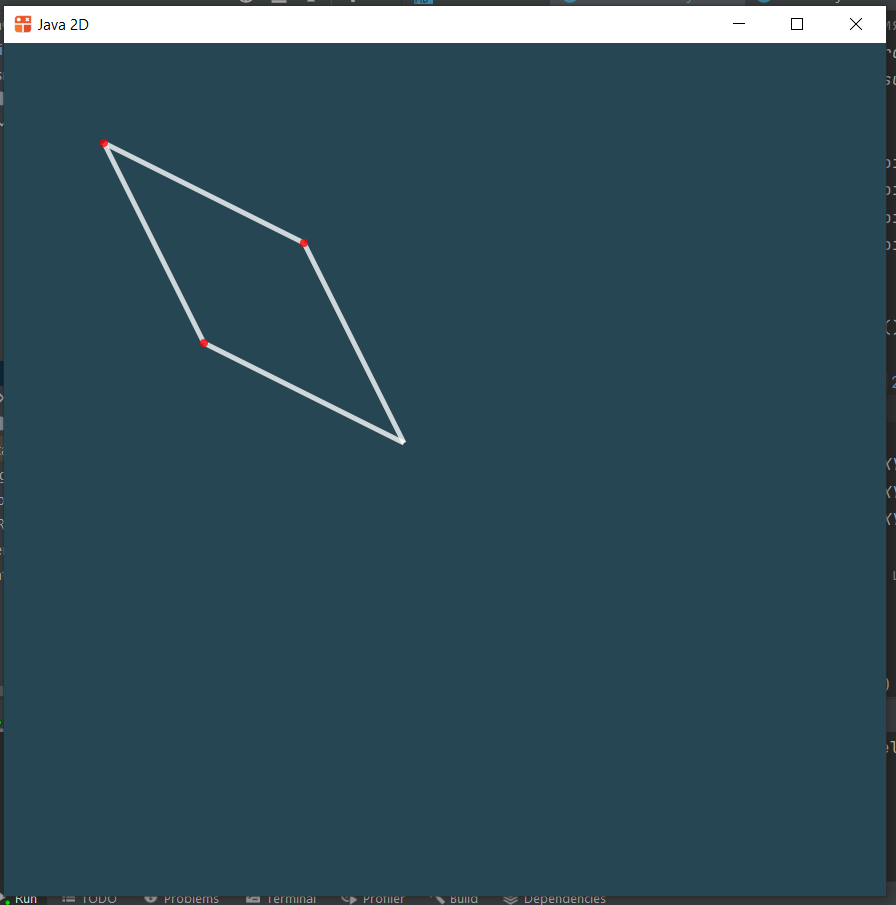
example

Угол

Угол задается точкой-вершиной и двумя точками, через которые проходят его лучи, выходящие из вершины. Угол между лучами меньше 180 градусов.

Чтобы нарисовать угол, нам точно так же как в линии нужно определить вектор, ведущий из одной точки в другую, а потом продлить так, чтобы прибавляя его к вершине мы получили точку, которая будет находиться за границей экрана. Правда, здесь нужно будет продлевать только по одну сторону от вершины, но в направлении каждой из точек. При этом каждое из направления определяется по своей опорной точке

   // добавляем угол
        primitives.add((canvas, windowCS, p) -> {
            // вершина угла
            Vector2i pointA = new Vector2i(400, 400);
            // опорные точки
            Vector2i pointB = new Vector2i(100, 200);
            Vector2i pointC = new Vector2i(500, 300);

            // определяем вектор смещения
            Vector2i AB = Vector2i.subtract(pointB, pointA);
            Vector2i AC = Vector2i.subtract(pointC, pointA);

            // получаем максимальную длину отрезка на экране, как длину диагонали экрана
            int maxDistance = (int) windowCS.getSize().length();
            // получаем новые точки для рисования, которые гарантируют, что линия
            // будет нарисована до границ экрана
            Vector2i renderPointB = Vector2i.sum(pointA, Vector2i.mult(AB, maxDistance));
            Vector2i renderPointC = Vector2i.sum(pointA, Vector2i.mult(AC, maxDistance));

            // рисуем его стороны
            canvas.drawLine(pointA.x, pointA.y, renderPointB.x, renderPointB.y, p);
            canvas.drawLine(pointA.x, pointA.y, renderPointC.x, renderPointC.y, p);

            // сохраняем цвет рисования
            int paintColor = p.getColor();
            // задаём красный цвет
            p.setColor(Misc.getColor(200, 255, 0, 0));

            // рисуем опорные точки
            canvas.drawRRect(RRect.makeXYWH(pointA.x - 4, pointA.y - 4, 8, 8, 4), p);
            canvas.drawRRect(RRect.makeXYWH(pointB.x - 4, pointB.y - 4, 8, 8, 4), p);
            canvas.drawRRect(RRect.makeXYWH(pointC.x - 4, pointC.y - 4, 8, 8, 4), p);

            // восстанавливаем исходный цвет рисования
            p.setColor(paintColor);
        });

Получим рисование угла

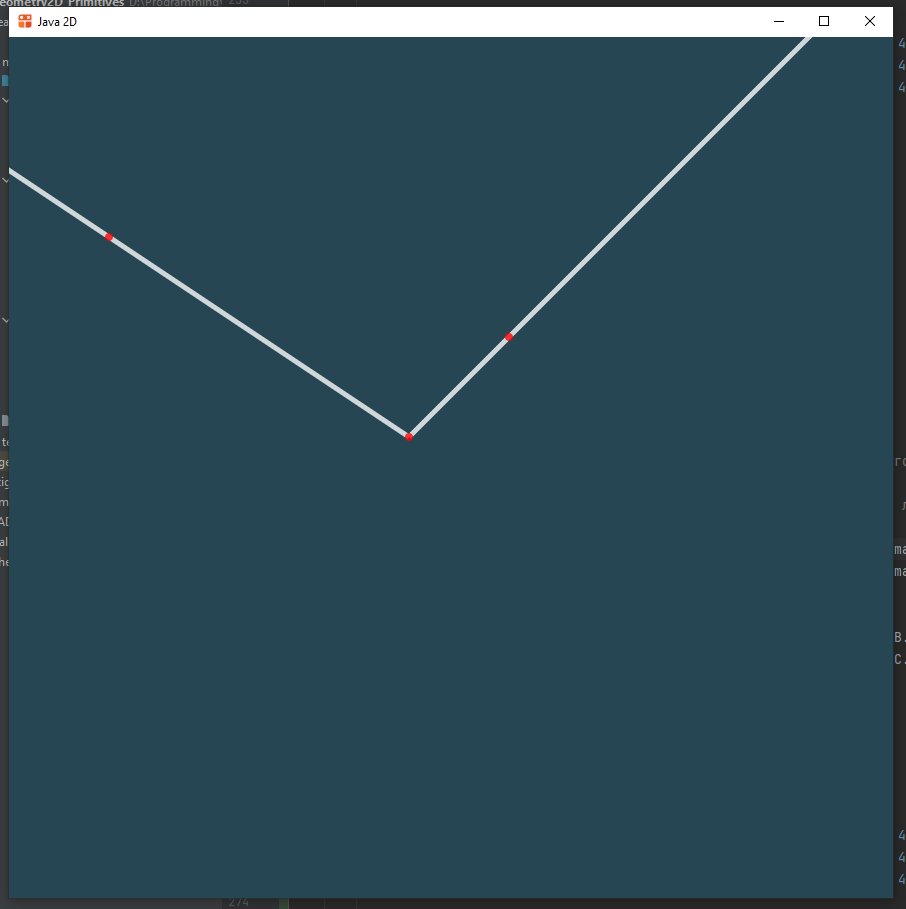
example

Полоса

Полоса - это широкая линия с заданной толщиной. Она задается прямой с помощью двух опорных точек, лежащей на ней и толщиной.

Для неё нам нужно определить сначала вектор направления по двум точкам, взять от него перпендикуляр и сместиться вдоль него на половину толщины полосы и в противоположную сторону. Так мы получим опорные точки, отложив от которых вектор направления, умноженный на длину диагонали экрана мы уже получим точки для рисования линии, как в соответствующем пункте.

        ...
        // добавляем полосу
        primitives.add((canvas, windowCS, p) -> {
            // вершина угла
            Vector2i pointA = new Vector2i(400, 400);
            // опорные точки
            Vector2i pointB = new Vector2i(100, 200);
            // отрезок AB
            Vector2i AB = Vector2i.subtract(pointB, pointA);
            // толщина линии
            double width = 40;
            // вектор направления для откладывания ширины
            Vector2i widthDirection = new Vector2d(AB).rotated(Math.PI / 2).norm().mult(width / 2).intVector();

            // получаем максимальную длину отрезка на экране, как длину диагонали экрана
            int maxDistance = (int) windowCS.getSize().length();
            // создаём вектор направления для рисования условно бесконечной полосы
            Vector2i direction = new Vector2d(AB).norm().mult(maxDistance).intVector();

            // получаем опорные точки для откладывания направления
            Vector2i basePointA = Vector2i.sum(pointA, widthDirection);
            Vector2i basePointB = Vector2i.subtract(pointA, widthDirection);

            // получаем точки рисования
            Vector2i renderPointA = Vector2i.sum(basePointA, direction);
            Vector2i renderPointD = Vector2i.subtract(basePointA, direction);
            Vector2i renderPointB = Vector2i.sum(basePointB, direction);
            Vector2i renderPointC = Vector2i.subtract(basePointB, direction);

            // рисуем отрезки
            canvas.drawLine(renderPointA.x, renderPointA.y, renderPointB.x, renderPointB.y, p);
            canvas.drawLine(renderPointB.x, renderPointB.y, renderPointC.x, renderPointC.y, p);
            canvas.drawLine(renderPointC.x, renderPointC.y, renderPointD.x, renderPointD.y, p);
            canvas.drawLine(renderPointD.x, renderPointD.y, renderPointA.x, renderPointA.y, p);
            // сохраняем цвет рисования
            int paintColor = p.getColor();
            // задаём красный цвет
            p.setColor(Misc.getColor(200, 255, 0, 0));
            // рисуем исходные точки
            canvas.drawRRect(RRect.makeXYWH(pointA.x - 4, pointA.y - 4, 8, 8, 4), p);
            canvas.drawRRect(RRect.makeXYWH(pointB.x - 4, pointB.y - 4, 8, 8, 4), p);
            // задаём зелёный цвет
            p.setColor(Misc.getColor(200, 0, 255, 0));
            // рисуем опорные точки
            canvas.drawRRect(RRect.makeXYWH(basePointA.x - 4, basePointA.y - 4, 8, 8, 4), p);
            canvas.drawRRect(RRect.makeXYWH(basePointB.x - 4, basePointB.y - 4, 8, 8, 4), p);
            // восстанавливаем исходный цвет рисования
            p.setColor(paintColor);
        });
        ...

Проверим рисование полосы

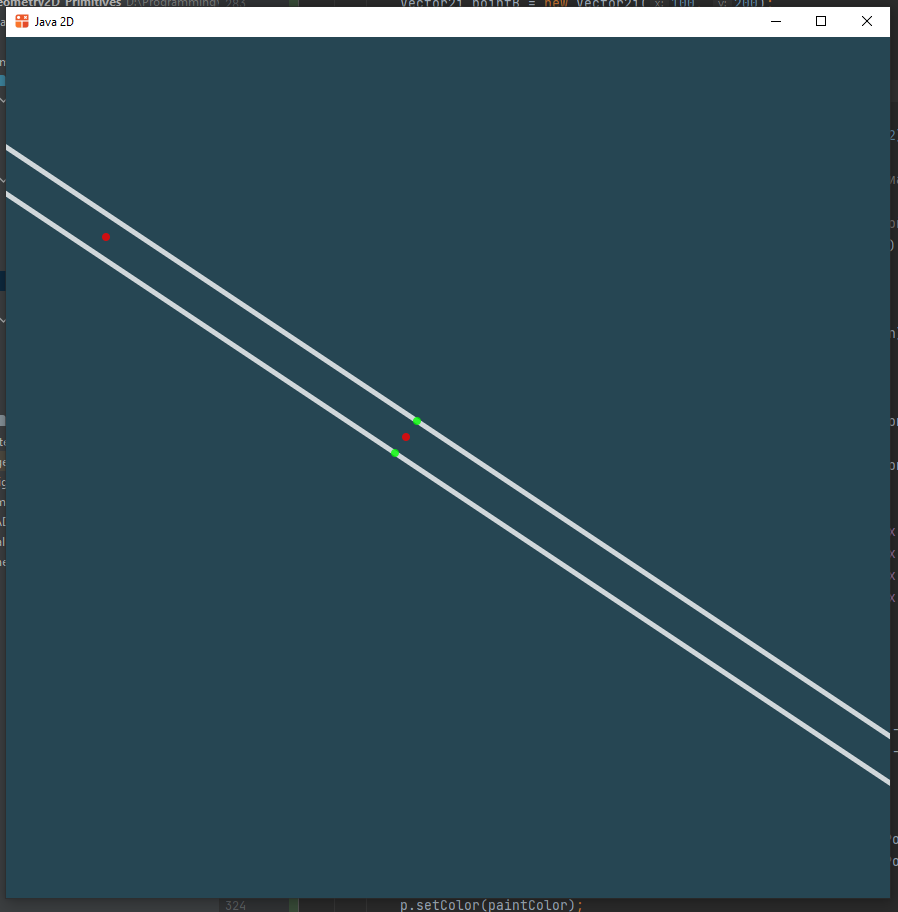
example

Всё работает как нужно.

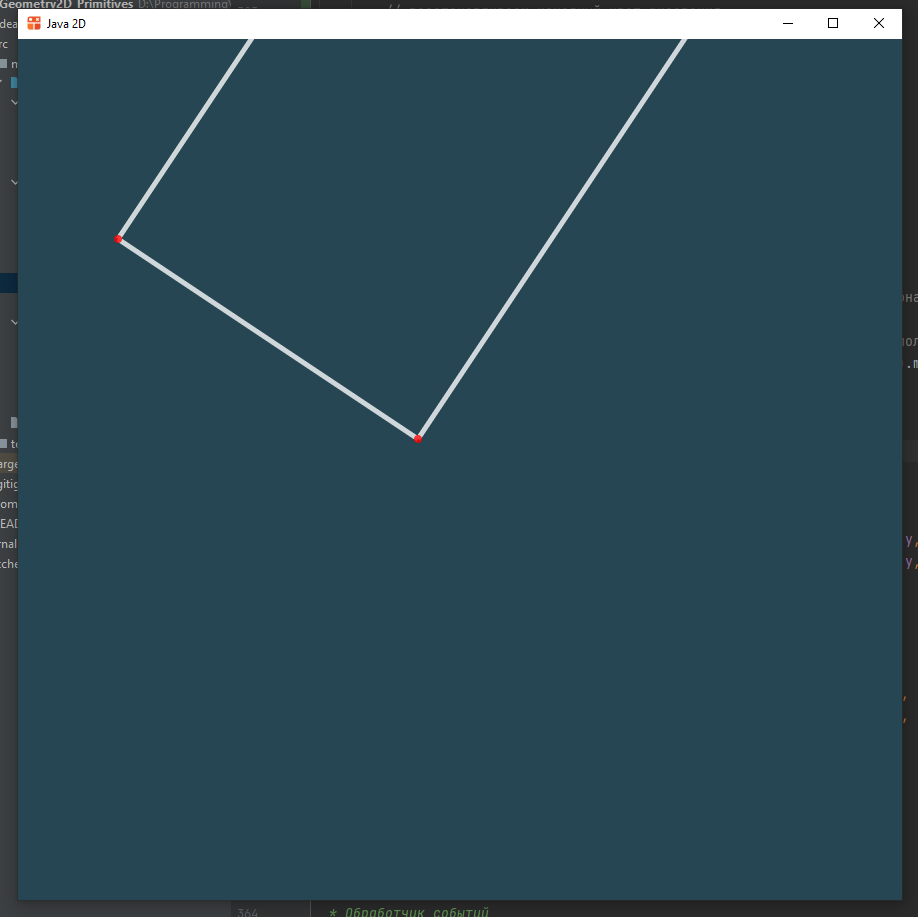
Широкий луч

Широкий луч - это прямоугольник с одной из сторон, находящейся в бесконечности.

Он задается двумя точками, являющимися вершинами одной из сторон прямоугольника. Направление "луча" получается поворотом на $\frac{\pi}{2}$ вектора, проведенного из первой точки во вторую.

Этот примитив рисуется очень похожим способом, но точки за экраном нужно создать только в одном направлении. Вместо построения в противоположную сторону условно бесконечных отрезков мы просто нарисуем отрезок, соединяющий две опорные точки.

Добавим теперь примитив

        ...
        // широкий луч
        primitives.add((canvas, windowCS, p) -> {
            // вершина угла
            Vector2i pointA = new Vector2i(400, 400);
            // опорные точки
            Vector2i pointB = new Vector2i(100, 200);
            // отрезок AB
            Vector2i AB = Vector2i.subtract(pointB, pointA);

            // получаем максимальную длину отрезка на экране, как длину диагонали экрана
            int maxDistance = (int) windowCS.getSize().length();
            // создаём вектор направления для рисования условно бесконечной полосы
            Vector2i direction = new Vector2d(AB).norm().rotated(Math.PI / 2).mult(maxDistance).intVector();

            // получаем точки рисования
            Vector2i renderPointC = Vector2i.sum(pointA, direction);
            Vector2i renderPointD = Vector2i.sum(pointB, direction);

            // рисуем отрезки
            canvas.drawLine(pointA.x, pointA.y, pointB.x, pointB.y, p);
            canvas.drawLine(pointA.x, pointA.y, renderPointC.x, renderPointC.y, p);
            canvas.drawLine(pointB.x, pointB.y, renderPointD.x, renderPointD.y, p);
            // сохраняем цвет рисования
            int paintColor = p.getColor();
            // задаём красный цвет
            p.setColor(Misc.getColor(200, 255, 0, 0));
            // рисуем исходные точки
            canvas.drawRRect(RRect.makeXYWH(pointA.x - 4, pointA.y - 4, 8, 8, 4), p);
            canvas.drawRRect(RRect.makeXYWH(pointB.x - 4, pointB.y - 4, 8, 8, 4), p);
            // восстанавливаем исходный цвет рисования
            p.setColor(paintColor);
        });
        ...

Получим рисование широкого луча

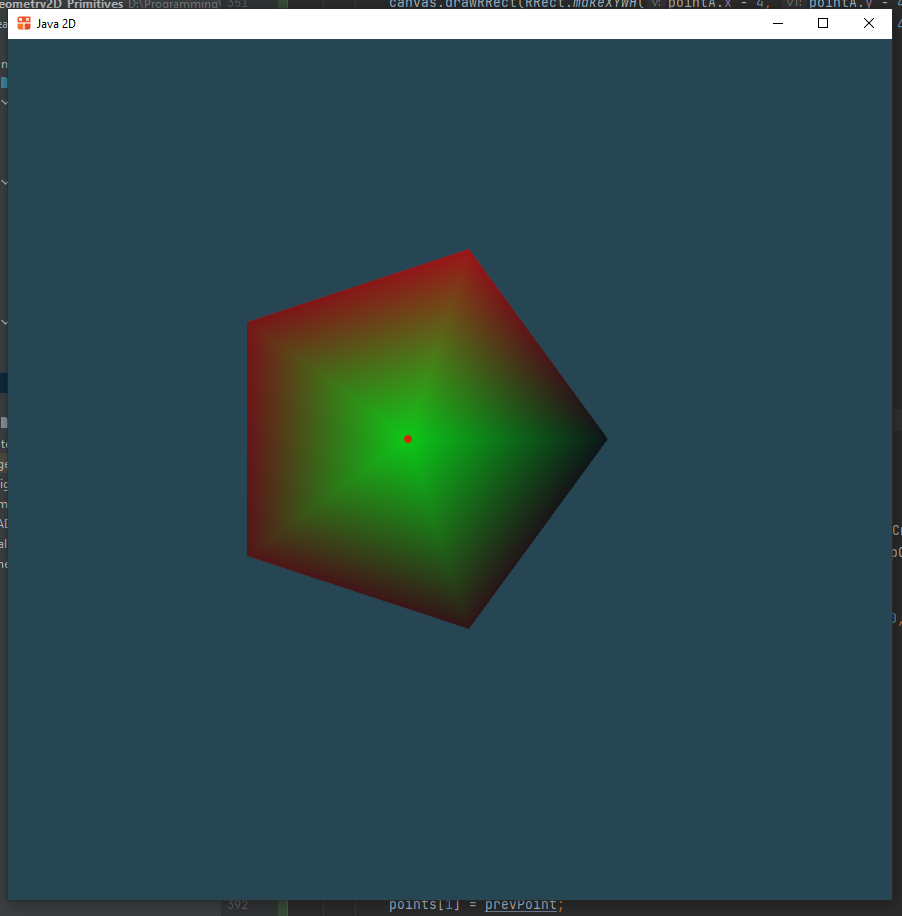
example

Многоугольник

В некоторых задачах для отображения ответа необходимо будет нарисовать закрашенный многоугольник. Если стоит задача нарисовать его контур, то решить её можно просто вызвав метод drawLine() для каждых двух соседних точек.

Если же на нужно нарисовать именно закрашенный многоугольник, то здесь обычные методы не подходят.

В реальных графических приложениях редко рисуют каждый примитив по-отдельности. Чаще всего используют пакетный метод рисования полигонами. Полигоном называют фигуру, разбитую на треугольники.

Т.е. вместо каждого примитива мы просто будем указывать точки и порядок построения по ним треугольников.

Чтобы нарисовать многоугольник, лучше всего подходит метод canvas.drawTriangleFan().

В качестве аргументов ему следует передать массив точек Point. Не следует путать этот класс с тем, что мы определили в прошлой задаче. Этот класс Point поставляется вместе с движком. По сути он просто хранит две координаты и обладает некоторыми полезными для движка функциями.

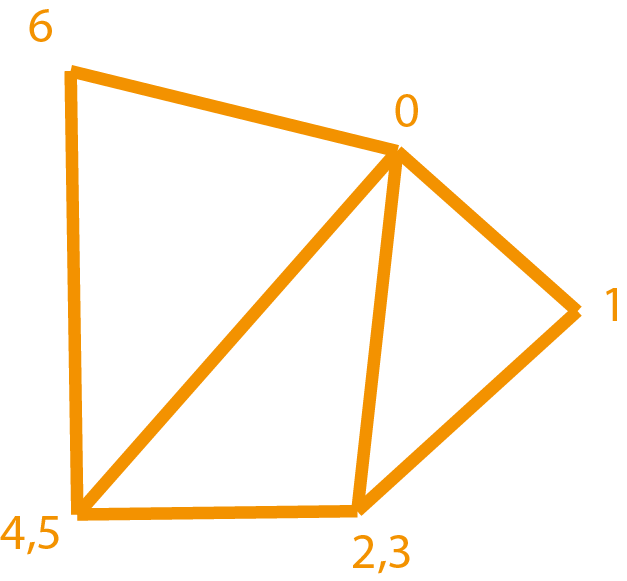
example

Массив точек и цветов устроен следующим образом: нулевой элемент задаёт общую точку для всех треугольников, первую вершину, потом идут пары элементов, задающие оставшиеся две опорные точки для каждого из треугольников.

Также он принимает в качестве аргумента массив цветов. Для каждой точки можно задать свой цвет, тогда получим градиентную заливку.

Чтобы нарисовать именно многоугольник в таком пакетном режиме, нам нужно определить центральную точку, которую мы сделаем первой, и от которой будем строить все полигоны, составляющие многоугольник.

Эта точка равна просто среднему арифметическому всех остальных.

Пропишем эту логику в отдельном классе многоугольника Polygon. У движка есть свой класс с таким же названием, поэтому будьте внимательны при импорте.

Polygon.java

package app;
package app;


import io.github.humbleui.skija.Canvas;
import io.github.humbleui.skija.Paint;
import io.github.humbleui.skija.Point;
import misc.Misc;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/**
 * Класс многоугольника
 */
public class Polygon {
    /**
     * Список точек
     */
    private final List<Point> pointList;
    /**
     * Список цветов
     */
    private final List<Integer> colorList;
    /**
     * Массив цветов для рисования
     */
    private int[] renderColors;
    /**
     * Массив точек для рисования
     */
    Point[] renderPoints;

    /**
     * Конструктор многоугольника
     */
    public Polygon() {
        pointList = new ArrayList<>();
        colorList = new ArrayList<>();
    }

    /**
     * Добавить точку в многоугольник
     *
     * @param x     координата X
     * @param y     координата Y
     * @param color цвет
     */
    public void add(int x, int y, int color) {
        pointList.add(new Point(x, y));
        colorList.add(color);
    }

    /**
     * Рассчитать точки и цвета для рисования
     */
    public void calculate() {
        // кол-во точек
        int n = pointList.size();
        // 2n нужно для хранения для каждого треугольника двух опорных точек
        // ещё один элемент(с индексом 0) нужен для хранения общей третьей опорной
        // точки
        renderColors = new int[n * 2 + 1];
        renderPoints = new Point[n * 2 + 1];

        // переменные для нахождения центра многоугольника
        float sumX = 0;
        float sumY = 0;

        // перебираем все вершины многоугольника кроме последней
        for (int i = 0; i < n - 1; i++) {
            // прибавляет координаты рассматриваемой точки к сумме
            sumX += pointList.get(i).getX();
            sumY += pointList.get(i).getY();
            // заполняем точки рисования
            renderPoints[i * 2 + 1] = pointList.get(i);
            renderPoints[i * 2 + 2] = pointList.get(i + 1);
            // заполняем цвета рисования
            renderColors[i * 2 + 1] = colorList.get(i);
            renderColors[i * 2 + 2] = colorList.get(i + 1);
        }

        // прибавляет координаты последней точки к сумме
        sumX += pointList.get(n - 1).getX();
        sumY += pointList.get(n - 1).getY();

        // заполняем точки рисования последнего треугольника
        renderPoints[n * 2 - 1] = pointList.get(n - 1);
        renderPoints[n * 2] = pointList.get(0);
        // заполняем цвета рисования последнего треугольника
        renderColors[n * 2 - 1] = colorList.get(n - 1);
        renderColors[n * 2] = colorList.get(0);

        // задаём общую опорную точку
        renderPoints[0] = new Point(sumX / n, sumY / n);
        renderColors[0] = Misc.getColor(180, 0, 255, 0);
    }

    /**
     * Нарисовать многоугольник
     *
     * @param canvas область рисования
     * @param p      перо
     */
    public void paint(Canvas canvas, Paint p) {
        canvas.drawTriangleFan(renderPoints, renderColors, p);
    }

    /**
     * Получить центр многоугольника
     *
     * @return центр многоугольника
     */
    public Point getCenter() {
        return renderPoints[0];
    }
}

Теперь добавим многоугольник на панель примитивов:

        // многоугольник
        primitives.add((canvas, windowCS, p) -> {
            // кол-во точек полигона
            int pCnt = 5;
            // центр полигона
            Vector2i center = new Vector2i(500, 500);
            // радиус
            float rad = 200;
            // создаём полигон
            Polygon polygon = new Polygon();

            // заполняем массив
            for (int i = 0; i < pCnt; i++) {
                // добавляем новую точку
                polygon.add(
                        center.x + (int) (rad * Math.cos(2 * Math.PI / pCnt * i)),
                        center.y + (int) (rad * Math.sin(2 * Math.PI / pCnt * i)),
                        Misc.getColor(230, 255 * i / pCnt, 0, 0)
                );
            }
            // рассчитываем полигон
            polygon.calculate();
            // рисуем полигон
            polygon.paint(canvas, p);
            
            // сохраняем цвет рисования
            int paintColor = p.getColor();
            // задаём синий цвет
            p.setColor(Misc.getColor(140, 0, 0, 255));
            Point pCenter = polygon.getCenter();
            canvas.drawRRect(RRect.makeXYWH(pCenter.getX() - 4, pCenter.getY() - 4, 8, 8, 4), p);
            // восстанавливаем цвет
            p.setColor(paintColor);
        });

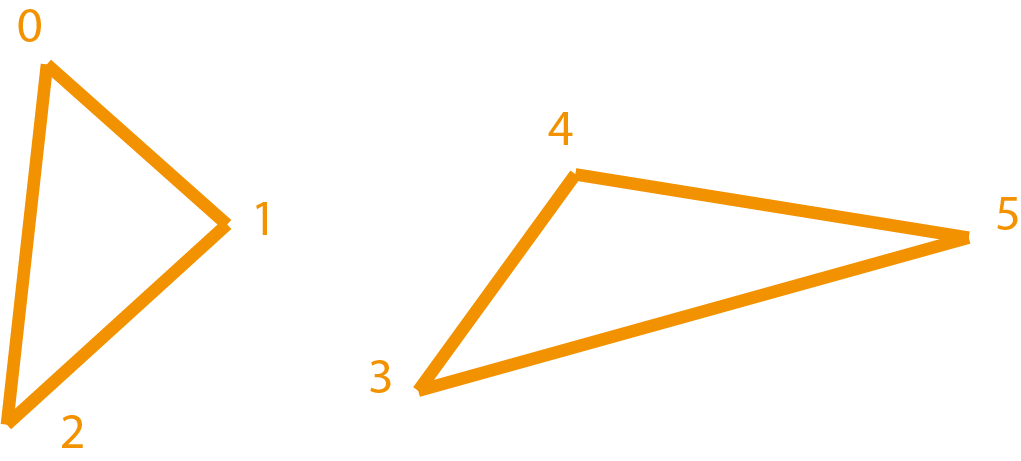
example

Если вы хотите рисовать каждый треугольник по отдельности, то вам будет нужен метод canvas.drawTriangles(). Аргументы у него такие же, но заполнять массивы следует по другой логике. Для этого метода точки задаются просто тройками. Для трёх треугольников нам нужно будет указать девять точек, а для пяти - пятнадцать.

example

Исходники этого приложения можно скачать здесь

Эллипс

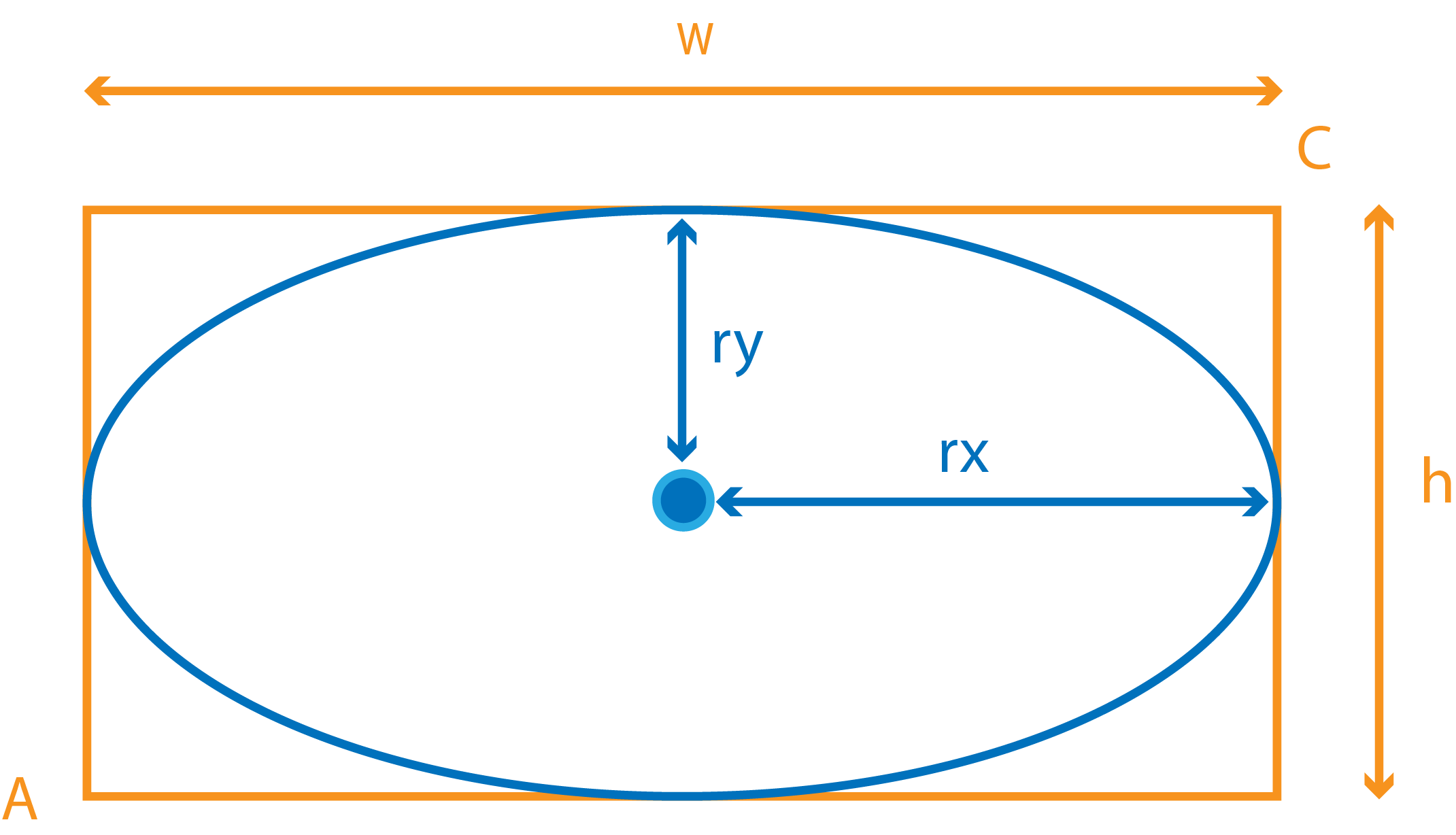
Параллельный эллипс задается "параллельным" прямоугольником, в который вписан.

Мы уже написали код для рисования растянутой окружности по её центру и радиусам вдоль осей координат. Поэтому в этом и следующем пункте нам достаточно свести задачу к рисованию растянутой окружности.

Пусть $w$ - ширина опорного параллельного прямоугольника, а $h$ - высота, тогда

w = |C_x-A_x|\\ h = |C_y-A_y|

Координаты центра прямоугольника совпадают с координатами центра эллипса. Обозначим центр эллипса буквой $O$ , тогда его координаты можно получить прибавив к положению вершины $A$ половину вектора $\vec{AC}$

O_x = A_x+(C_x-A_x)/2\\ O_y = A_y+(C_y-A_y)/2

Радиусы вдоль осей координат в два раза меньше соответствующих сторон:

r_x = w/2\\ r_y = h/2

example

В этом примитиве нам понадобится взять половину целочисленного вектора. Для этого напишем метод деления целочисленного вектора на число:

    /**
     * Разделить вектор на число
     *
     * @param v вектор
     * @param d число
     * @return результат деления
     */
    public static Vector2i div(Vector2i v, int d) {
        return new Vector2i(v.x / d, v.y / d);
    }

Теперь пропишем сам примитив

        // добавляем параллельный эллипс
        primitives.add((canvas, windowCS, p) -> {
            // левая верхняя вершина
            Vector2i pointA = new Vector2i(200, 100);
            // правая нижняя
            Vector2i pointC = new Vector2i(300, 500);
            // находим вектор AC
            Vector2i AC = Vector2i.subtract(pointC, pointA);
            // центр окружности
            Vector2i center = Vector2i.sum(pointA, Vector2i.div(AC, 2));
            // радиус вдоль оси x
            int radX = Math.abs(AC.x) / 2;
            // радиус вдоль оси y
            int radY = Math.abs(AC.y) / 2;
            // кол-во отсчётов цикла
            int loopCnt = 40;
            // создаём массив координат опорных точек
            float[] points = new float[loopCnt * 4];
            // запускаем цикл
            for (int i = 0; i < loopCnt; i++) {
                // x координата первой точки
                points[i * 4] = (float) (center.x + radX * Math.cos(Math.PI / 20 * i));
                // y координата первой точки
                points[i * 4 + 1] = (float) (center.y + radY * Math.sin(Math.PI / 20 * i));

                // x координата второй точки
                points[i * 4 + 2] = (float) (center.x + radX * Math.cos(Math.PI / 20 * (i + 1)));
                // y координата второй точки
                points[i * 4 + 3] = (float) (center.y + radY * Math.sin(Math.PI / 20 * (i + 1)));
            }
            // рисуем линии
            canvas.drawLines(points, p);
            

            // сохраняем цвет рисования
            int paintColor = p.getColor();
            // задаём красный цвет
            p.setColor(Misc.getColor(200, 255, 0, 0));

            // рассчитываем опорные точки прямоугольника
            Vector2i pointB = new Vector2i(pointA.x, pointC.y);
            Vector2i pointD = new Vector2i(pointC.x, pointA.y);

            // рисуем его стороны
            canvas.drawLine(pointA.x, pointA.y, pointB.x, pointB.y, p);
            canvas.drawLine(pointB.x, pointB.y, pointC.x, pointC.y, p);
            canvas.drawLine(pointC.x, pointC.y, pointD.x, pointD.y, p);
            canvas.drawLine(pointD.x, pointD.y, pointA.x, pointA.y, p);
            // восстанавливаем исходный цвет рисования
            p.setColor(paintColor);

        });

Для самопроверки рисуется ещё и опорный параллельный прямоугольник

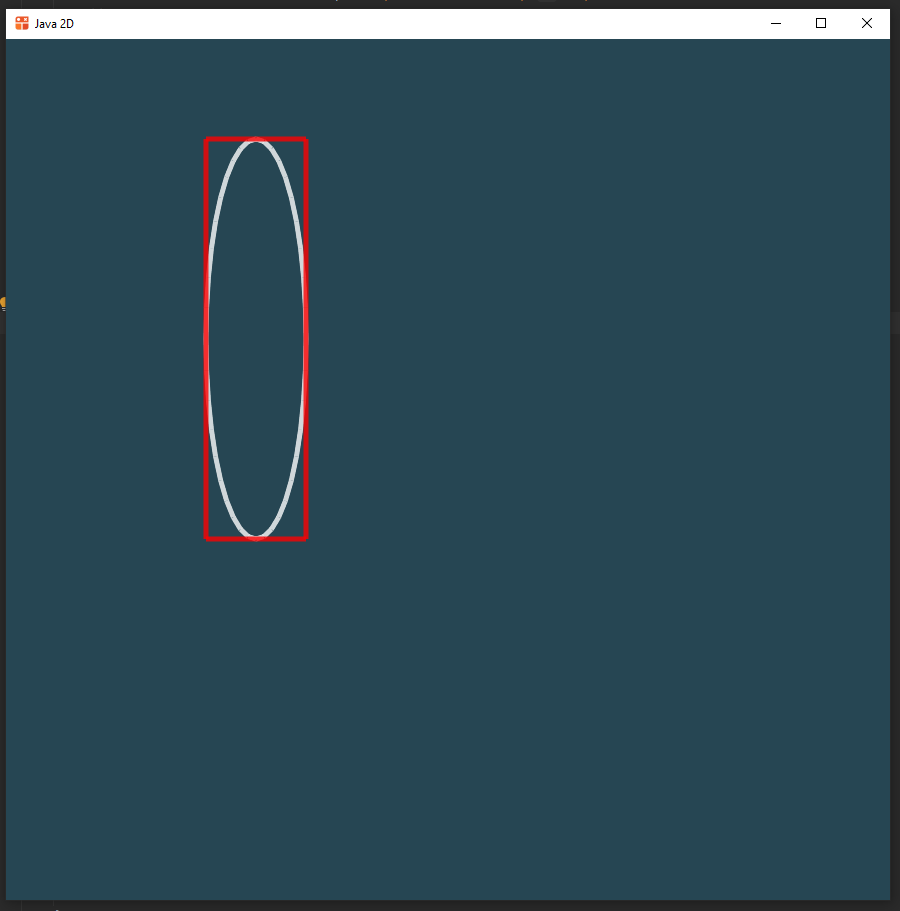
example

Метод Монте-Карло

В части задач нужно находить площадь пересечения. Лучше всего с этим справляется метод Монте-Карло.

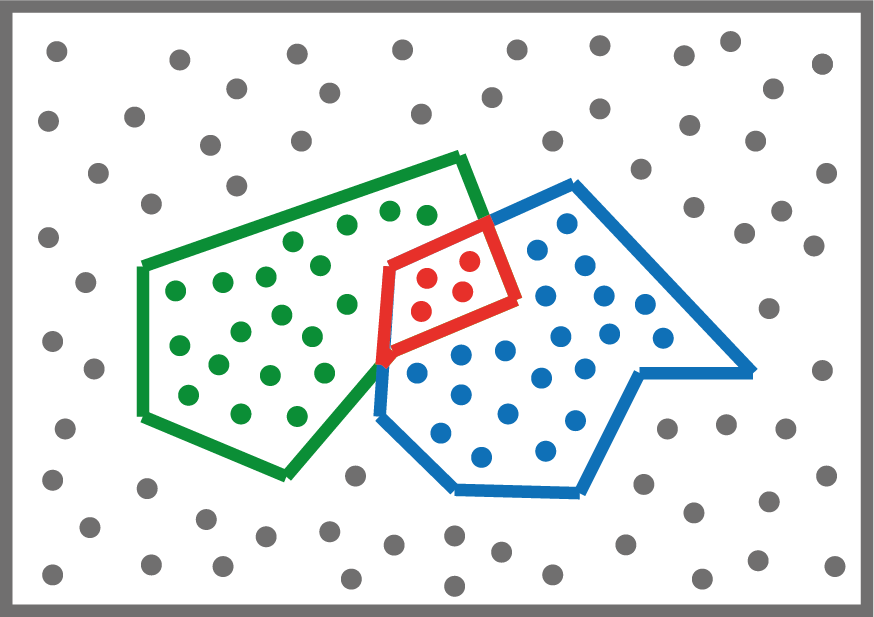
example

Его идея заключается в том, что мы генерируем множество случайных точек, а потом считаем, какая часть из них принадлежит той или иной фигуре, их пересечению. При достаточно большом количестве точек отношение количеств точек внутри той или иной фигуры равно отношению площадей этих фигур.

Поэтому если принять площадь экрана за исходную $S$ , тогда площадь любой фигуры $S_f$ будет равна

S_f = S\frac{C_f}{C},

где $C$ - общее число случайных точек, $C_f$ - кол-во точек внутри фигуры

Точка​

Прямая​

Треугольник​

Окружность​

Параллельный прямоугольник​

Прямоугольник​

Параллелограмм​

Угол​

Полоса​

Широкий луч​

Многоугольник​

Эллипс​

Метод Монте-Карло​

Точка

Прямая

Треугольник

Окружность

Параллельный прямоугольник

Прямоугольник

Параллелограмм

Угол

Полоса

Широкий луч

Многоугольник

Эллипс

Метод Монте-Карло